6 janvier 1918 – Georg Cantor le créateur de la théorie des ensembles en mathématique

Georg Cantor est à l’origine (1897) du premier Congrès International des MathématiciensLe mathématicien de génie qui a ouvert pour les mathématiques le paradis de l’infini.Georg Cantor était un mathématicien d’origine russe qui peut être considéré comme le fondateur de la théorie des ensembles et a introduit le concept de nombres infinis avec sa découverte des nombres cardinaux. Il a également fait progresser l’étude des séries trigonométriques.La vie et les contributions de Georg Cantor aux mathématiquesLes débuts de Georg Cantor

Georg Cantor (1845-1918) est né le 3 Mars 1845 dans la colonie marchande occidentale de Saint-Pétersbourg, en Russie, en tant qu’enfant aîné de son père et son nom complet était Georg Ferdinand Ludwig Philipp Cantor. Son père était un marchand juif danois qui s’était converti au protestantisme et sa mère une catholique danoise. Il a fait ses études primaires en cours particuliers dans la mission luthérienne. Il a vécu dans la ville jusqu’à l’âge de onze ans et sa famille a déménagé à Francfort allemand lorsque son père est tombé malade pour un climat plus chaud en 1856 où il devait passer le reste de sa vie. Le talent mathématique de Georg Cantor a commencé à se manifester à l’âge de quinze ans alors qu’il était dans un gymnase. Son père voulait qu’il soit ingénieur mais il n’aimait pas ça car il aimait les mathématiques ; il n’a pas eu le courage de parler à son père de son intérêt pour les mathématiques

Avant de rejoindre le collège, il a demandé à son père de lui permettre de poursuivre des cours de mathématiques et il a accepté. Il rejoint l’Université de Zurich en 1862 et est transféré l’année suivante après la mort de son père à l’Université de Berlin où il étudie les mathématiques, la philosophie et la physique. En 1867, il obtint un doctorat mais il n’obtint pas un bon emploi et fut forcé de travailler comme conférencier non rémunéré et plus tard comme professeur assistant à l’Université Backwater de Halle. Il épousa Valley Guttman en 1874 et eut six enfants dont le dernier né en 1888 avant de mourir le 6 janvier 1918.Ses apports

Au cours de sa vie, Georg Cantor a prouvé plusieurs concepts en mathématiques que d’autres mathématiciens avant lui ont été incapables de prouver. Cantor a été encouragé par son ami de Halle qui travaillait sur les séries trigonométriques à travailler sur l’unicité des séries infinies. En 1873, il a pu prouver que les nombres rationnels sont dénombrables, il a ajouté que les nombres algébriques qui sont des racines, des carrés et des racines carrées d’équation polynomiale à coefficients entiers sont dénombrables. Il a publié son premier article sur la théorie des ensembles en 1874 où il a prouvé que l’ensemble des nombres entiers avait un nombre égal de membres. Set Theory – Todd Decker Il a également proposé l’argument selon lequel les nombres réels ne sont pas dénombrables, ce qu’il a prouvé. Il a déclaré que les nombres transcendantaux sont des nombres irrationnels qui ne sont pas la racine, le carré ou la racine carrée d’une équation polynomiale ayant des coefficients entiers. Georg a pu montrer que l’intervalle entre zéro et un est indénombrable. Il est le seul mathématicien qui a pu montrer que presque tous les nombres sont transcendantaux en prouvant que les nombres réels ne sont pas dénombrables tout en prouvant que les nombres algébriques étaient dénombrables, il a également montré que l’ensemble de tous les sous-ensembles d’un ensemble donné est plus grand que l’original Positionner. L’introduction du concept de premier ensemble dérivé fut son initiative. Cantor a également montré que l’union de deux ensembles dénombrables devrait également être dénombrable et faire passer l’existence de nombres indénombrables. Georg Cantor a été le premier à discuter de l’hypothèse du continu qui stipule qu’il existe un ensemble de nombres dont la puissance est supérieure à celle des naturels et inférieure à celle des réels, il l’a essayé mais tout était en vain car il a pu prouver et le réfuter. Golden et Paul Cohen en 1963 ont déclaré que l’hypothèse peut être prouvée ou réfutée.Conclusion

Le travail de Cantor a reçu beaucoup d’opposition de la part des éditoriaux de l’époque mais il a pu leur prouver tous ses arguments, c’est en raison de son appartenance religieuse qu’il a pu résister et gérer toutes les oppositions qui se sont présentées à ses côtés.

Laissé Georg étudier les mathématiques. En 1862, Georg Cantor entre à l’Université de Zurich pour être transféré l’année suivante à l’Université de Berlin après la mort de son père. A Berlin, il étudie les mathématiques, la philosophie et la physique. Là, il a étudié avec certains des plus grands mathématiciens de l’époque, dont Kronecker et Weierstrass. Après avoir obtenu son doctorat en 1867 à Berlin, il n’a pas pu trouver un bon emploi et a été contraint d’accepter un poste de chargé de cours non rémunéré, puis de professeur adjoint à l’Université de Halle en 1869. En 1874, il se marie et a six enfants. C’est cette même année 1874 que Cantor publie son premier article sur la théorie des ensembles. Alors qu’il étudiait un problème d’analyse, il avait approfondi ses fondements, en particulier les ensembles et les ensembles infinis. Ce qu’il trouva le déconcerta. Dans une série d’articles de 1874 à 1897, il a pu prouver que l’ensemble des nombres entiers avait un nombre égal de membres que l’ensemble des nombres pairs, des carrés, des cubes et des racines des équations ; que le nombre de points dans un segment de ligne est égal au nombre de points dans une ligne infinie, un plan et tout l’espace mathématique ; et que le nombre de nombres transcendantaux, des valeurs telles que pi (3,14159) et e (2,71828) qui ne peuvent jamais être la solution d’une équation algébrique, était beaucoup plus grand que le nombre d’entiers. Did Cantor's set theory have any impact on fields other than mathematics - like physics, philosophy, biology,chemistry,economics etc? If yes, how do people today view this impact? - Quora Avant en mathématiques, l’infini était un sujet sacré. Auparavant, Gauss avait déclaré que l’infini ne devait être utilisé que comme une façon de parler et non comme une valeur mathématique. La plupart des mathématiciens ont suivi ses conseils et sont restés à l’écart. Cependant, Cantor ne le laisserait pas seul. Il considérait les ensembles infinis non pas simplement comme s’éternisant, mais comme des entités achevées, c’est-à-dire ayant un nombre réel mais infini de membres. Il a appelé ces nombres infinis réels des nombres transfinis. En considérant les ensembles infinis avec un nombre transfini de membres, Cantor a pu faire ses étonnantes découvertes. Pour son travail, il est promu professeur titulaire en 1879. Cependant, ses nouvelles idées lui ont également valu de nombreux ennemis. De nombreux mathématiciens n’accepteraient tout simplement pas ses idées révolutionnaires qui ont brisé leur monde sûr des mathématiques. L’un de ces critiques était Leopold Kronecker. Kronecker croyait fermement que les seuls nombres étaient des nombres entiers et que les nombres négatifs, les fractions, les imaginaires et surtout les nombres irrationnels n’avaient rien à voir avec les mathématiques. Il ne pouvait tout simplement pas gérer l’infini réel. Utilisant son prestige de professeur à l’Université de Berlin, il fit tout ce qu’il put pour réprimer les idées de Cantor et ruiner sa vie. Entre autres choses, il retarda ou supprima complètement les publications de Cantor et de ses partisans, minimisa ses idées devant ses étudiants et bloqua l’ambition de la vie de Cantor d’obtenir un poste à la prestigieuse université de Berlin. Cantor Set | Galileo Unbound Tous les mathématiciens n’étaient pas hostiles aux idées de Cantor. Certains grands noms tels que Karl Weierstrass et son ami de longue date Richard Dedekind ont soutenu ses idées et attaqué les actions de Kronecker. Cependant, ce n’était pas suffisant. Cantor ne pouvait tout simplement pas le supporter. Coincé dans une institution de troisième ordre, privé d’une reconnaissance bien méritée pour son travail et constamment attaqué par Kronecker, il subit la première de nombreuses dépressions nerveuses en 1884.

En 1885, Cantor continua d’étendre sa théorie des nombres cardinaux et des types d’ordre. Il a étendu sa théorie des types d’ordre de sorte que maintenant ses nombres ordinaux précédemment définis sont devenus un cas particulier. En 1895 et 1897, Cantor publie son double traité final sur la théorie des ensembles. Cantor prouve que si A et B sont des ensembles avec A équivalent à un sous-ensemble de B et B équivalent à un sous-ensemble de A alors A et B sont équivalents. Ce théorème a également été prouvé par Felix Bernstein et par Schröder.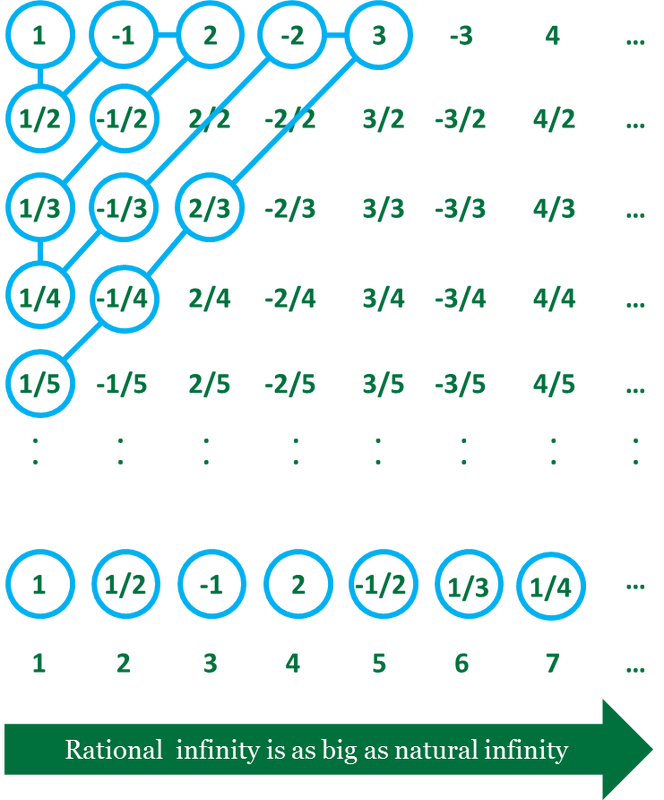 Splitting Infinity(ves): The Story of Georg Cantor - The Institution for Science Advancement Le reste de sa vie a été passé dans et hors des établissements psychiatriques et son travail a presque complètement cessé. Beaucoup trop tard pour qu’il puisse vraiment en profiter, sa théorie a finalement commencé à être reconnue au tournant du siècle. En 1904, il reçoit une médaille de la Royal Society of London et devient membre de la London Mathematical Society et de la Society of Sciences de Gottingen. Il mourut dans un hôpital psychiatrique le 6 janvier 1918. Aujourd’hui, les travaux de Cantor sont largement utilisés dans les nombreux domaines des mathématiques. Sa théorie sur les ensembles infinis a réinitialisé les fondements de presque tous les domaines mathématiques et a amené les mathématiques à leur forme moderne.

Infini

Presque tout le monde connaît le symbole de l’infini. Combien est infiniment nombreux ? À quelle distance est « d’ici à l’infini » ? Quelle est la taille de l’infini ? On ne peut pas compter jusqu’à l’infini. Pourtant, nous sommes à l’aise avec l’idée qu’il y a une infinité de nombres avec lesquels compter : peu importe la taille du nombre que vous pouvez trouver, quelqu’un d’autre peut en trouver un plus grand : ce nombre plus un ou plus deux, ou fois deux. Il n’y a tout simplement pas de plus grand nombre. Notes from the life of George Cantor. | Download Scientific Diagram L’infini est-il un nombre ? Existe-t-il quelque chose de plus grand que l’infini ? Que diriez-vous de l’infini plus un? Qu’est-ce que l’infini plus l’infini ? Qu’en est-il de l’infini multiplié par l’infini ? Les enfants pour qui le concept d’infini est tout nouveau posent des questions comme celle-ci et n’obtiennent généralement pas de réponses très satisfaisantes. Pour les adultes, ces questions ne semblent pas avoir beaucoup d’incidence sur la vie quotidienne, de sorte que leurs réponses insatisfaisantes ne semblent pas être un sujet de préoccupation. Au tournant du siècle, Cantor a appliqué les outils de la rigueur mathématique et de la déduction logique aux questions sur l’infini à la recherche de réponses satisfaisantes. Ses conclusions sont paradoxales par rapport à notre expérience quotidienne, mais elles sont mathématiquement fondées. Le monde de notre expérience quotidienne est fini. Nous ne pouvons pas dire exactement où se trouve la frontière, mais au-delà du fini, dans le domaine du transfini, les choses sont différentes.

Ensembles et théorie des ensembles Cantor est le fondateur de la branche des mathématiques appelée théorie des ensembles, qui est à la base d’une grande partie des mathématiques du XXe siècle. Au cœur de la théorie des ensembles se trouve une salle des miroirs – l’infini paradoxal. Georg Cantor était connu pour avoir dit : « Je le vois, mais je ne le crois pas », à propos d’une de ses preuves.

L’ensemble est l’objet mathématique que Cantor a scruté. Il a défini un ensemble comme toute collection d’objets bien distingués et bien définis considérés comme un tout unique. Une collection de plats assortis est un ensemble, ainsi qu’une collection de nombres. Même une collection de choses apparemment sans rapport comme, {télévision, oryctérope, voiture, 6} est un ensemble. Ils sont bien définis et peuvent être distingués les uns des autres.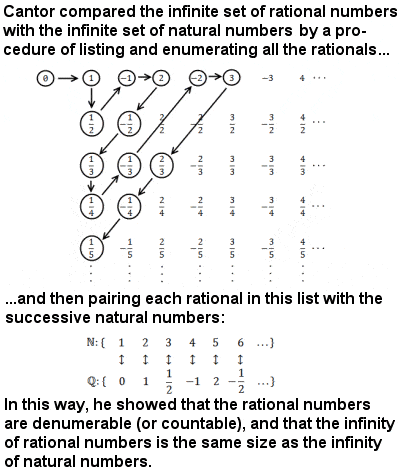 Georg Cantor - The Man Who Founded Set Theory Les ensembles peuvent être grands ou petits. Ils peuvent aussi être finis et infinis. Un ensemble fini a un nombre fini de membres. Peu importe combien il y en a, avec suffisamment de temps, vous pouvez tous les compter. Les résultats surprenants de Cantor sont survenus lorsqu’il a considéré des ensembles qui avaient un nombre infini de membres. Des ensembles tels que tous les nombres comptés ou tous les nombres pairs sont des ensembles infinis. Afin d’étudier les ensembles infinis, Cantor a d’abord formalisé de nombreuses choses qui sont intuitives et évidentes à propos des ensembles finis. Au début, il semble que ces formalisations ne soient qu’un tas de galères, une façon de compliquer des choses simples. Parce que les formalismes sont clairement corrects, cependant, ils fournissent un outil puissant pour examiner des choses qui ne sont pas si simples, intuitives ou évidentes.

Cantor avait besoin d’un moyen de comparer les tailles des ensembles, une méthode pour déterminer si les ensembles avaient le même nombre de membres. Si deux ensembles n’avaient pas le même nombre de membres, il avait besoin d’une méthode pour dire lequel était le plus grand. Bien sûr, c’est simple pour les ensembles finis. Vous comptez les membres dans les deux ensembles. Si le nombre est le même, ils sont de la même taille. Si le nombre de membres dans un ensemble est supérieur au nombre de membres dans l’autre, alors cet ensemble est plus grand. Cependant, vous ne pouvez pas compter les membres dans un ensemble infini, donc cette méthode ne fonctionnera pas pour comparer leurs tailles. S’il y a deux ensembles infinis, on doit avoir besoin d’un autre moyen pour savoir si l’un est plus grand. La notion formelle que Cantor a utilisée pour comparer les tailles des ensembles est l’idée d’une correspondance biunivoque. Une correspondance biunivoque associe les membres d’un ensemble aux membres d’un autre. On dit que les ensembles qui peuvent être appariés les uns aux autres dans ce sens ont la même cardinalité. On pourrait jumeler les éléments de l’ensemble imaginaire {télévision, oryctérope, voiture, 6} avec les chiffres {1,2,3,4}. Il est possible de faire cela pour qu’un membre de chaque ensemble soit jumelé avec un membre de l’autre, aucun membre n’est laissé de côté et aucun membre n’a plus d’un partenaire. Alors nous pouvons être sûrs que l’ensemble {1,2,3,4} a le même nombre de membres que l’ensemble {télévision, oryctérope, voiture, 6}.correspondance en tête à tête:

{Télévision, oryctérope, voiture, 6}

{1, 2, 3, 4}

Alors, qu’est-ce qui est plus gros ? Infini + X ? Infini + infini ? Ou l’infini (infini) ? Pour calculer quel est le plus grand chanteur, il a utilisé des ensembles et une correspondance biunivoque. Ces ensembles de correspondance biunivoque montrent que même si nous ajoutons une variable inconnue, multiplions par deux et mettons au carré un ensemble, les ensembles supérieur et inférieur restent toujours égaux. Puisque nous ne manquerons jamais de nombres, toute correspondance définie avec deux valeurs infinies sera égale. Tous ces ensembles ont clairement la même cardinalité puisque ses membres peuvent être mis en correspondance biunivoque les uns avec les autres indéfiniment. Ces ensembles sont dits dénombrables infinis et leur cardinalité est désignée par la lettre hébraïque aleph avec un indice zéro,

AUTRES INFINISCantor pensait qu’une fois que vous commencez à traiter avec des infinis, tout est de la même taille. Cela ne s’est pas avéré être le cas. Cantor a développé toute une théorie de l’arithmétique transfinie, l’arithmétique des nombres au-delà de l’infini. Bien que les tailles des ensembles infinis de nombres comptés, nombres pairs, nombres impairs, nombres carrés, etc., soient les mêmes, il existe d’autres ensembles, l’ensemble des nombres pouvant être exprimés sous forme de décimales, par exemple, qui sont plus grands. Les travaux de Cantor ont révélé qu’il existe des hiérarchies d’infinis toujours plus grands. Le plus grand s’appelle le Continuum. Certains mathématiciens qui vivaient à la fin du XIXe siècle ne voulaient pas du tout accepter son travail. Le fait que ses résultats soient si paradoxaux n’était pas tant le problème que le fait qu’il considérait des ensembles infinis. À cette époque, certains mathématiciens soutenaient que les mathématiques ne pouvaient considérer que des objets qui pouvaient être construits directement à partir des nombres comptés. Vous ne pouvez pas énumérer tous les éléments d’un ensemble infini, ont-ils dit, donc tout ce que vous dites sur les ensembles infinis n’est pas mathématique. Le plus puissant de ces mathématiciens était Leopold Kronecker qui a même développé une théorie des nombres qui n’incluait aucun nombre négatif.

Bien que Kronecker n’ait pas convaincu un grand nombre de ses contemporains d’abandonner toutes les conclusions reposant sur l’existence de nombres négatifs, le travail de Cantor était si révolutionnaire que l’argument de Kronecker selon lequel il « allait trop loin » semblait plausible. Kronecker était membre des comités de rédaction des importantes revues mathématiques de son époque et il a usé de son influence pour empêcher la publication d’une grande partie des travaux de Cantor de son vivant. Cantor ne savait pas au moment de sa mort que non seulement ses idées prévaudraient, mais qu’elles façonneraient le cours des mathématiques du XXe siècle.

Toroids within toroids, infinities within infinities ad infinitum. 🍩

“In one of his earliest papers, Georg Cantor proved that the set of real numbers is "more numerous" than the set of natural numbers; this showed, for the first time, that there exist infinite sets of different… pic.twitter.com/6Uq0i2XIRs

— inwyrd i (@inwyrdinfinitum) November 23, 2023

Il fallait probablement être un peu fou pour pouvoir imaginer que tous les ensembles infinis n’ont pas le même nombre d’éléments, pour définir des entiers infinis, les ordonner, et même les additionner. Georg Cantor (1845-1918) était ce fou-là, et ses idées révolutionnaires n’ont pas manqué de détracteurs. Georg Cantor est né le 3 mars 1845 à St Pétersbourg. Son père est commerçant prospère, sa mère est issue d’une famille de musiciens ; tous les deux sont très cultivés, et donnent à leur fils une éducation sérieuse, religieuse, et bercée par les arts. En 1846, la famille s’installe en Allemagne, où elle espère trouver un climat plus favorable à la santé du père.

Georg Cantor est le mathématicien de génie qui a ouvert pour les mathématiques le paradis de l’infini. Il a développé la théorie des ensembles qui permet de traiter tout objet mathématique comme un ensemble d’éléments déterminé, fini ou infini, et a introduit le concept de transfini, qui permet une arithmétique de l’infiniment grand. C’est une rupture avec deux mille ans d’histoire, saluée avec admiration par David Hilbert (1862-1943) qui voyait dans la théorie cantorienne « la fleur la plus admirable de l’esprit mathématique et l’une des plus sublimes réalisations de l’activité intellectuelle pure de l’homme ». D’Aristote à Descartes, en effet, on considère que l’infini ne peut être déterminé, c’est-à-dire qu’on ne peut lui assigner aucune quantité fixe. Bien plus, l’infini n’est inatteignable, car illimité. Pour Aristote, le mathématicien n’a d’ailleurs pas besoin de considérer des totalités infinies en acte, il lui suffit d’envisager des grandeurs plus grandes ou plus petites que toute grandeur donnée : l’infini du mathématicien est potentiel. Si l’on concevait une totalité infinie, ne devrait-on pas dire que ses parties aussi sont infinies ? Et ne serait-on pas alors conduit à dire qu’un infini, celui du tout, est plus grand qu’un autre, celui d’une de ses parties ? Y aurait-il donc différents infinis ? Comment les comparer ? Les paradoxes ne manquèrent pas de fleurir tandis que le thème de l’infinité divine impose, dès le Moyen Âge, la conception d’un infini qualitatif, le « vrai » infini de Descartes et de Spinoza, comme mode d’être d’un Dieu parfait et omnipotent. L’invention, au XVIIe siècle, du calcul infinitésimal qui introduit une manière d’ajouter, soustraire, diviser et multiplier des quantités infinies, ne ruine pas le substantialisme aristotélicien en vertu duquel on ne saurait reconnaître de réalité à un concept au référent « fluent », sans identité fixe. C’est ainsi que les quantités infinies reçoivent de Leibniz le statut de « fictions » dénotées par des symboles auxiliaires qui n’introduisent aucune irrégularité dans les calculs, une fois ceux-ci restreints aux quantités ordinaires.David Hilbert (1862-1943) souvent considéré comme un des plus grands mathématiciens du XXᵉ siècle a décrit le travail de Cantor comme suit : – le meilleur produit du génie mathématique et l’une des réalisations suprêmes de l’activité humaine purement intellectuelle.

Le Congrès International des Mathématiciens (CIM, ICM)Georg Cantor est à l’origine (1897) du premier Congrès International des Mathématiques CIM, plutôt abrégé en ICM : International Congress of Mathématiciens. Il se tint à Zürich. En 1900, le second eut lieu à Paris et resta célèbre par l’intervention de David Hilbert. Depuis 1936, c’est lors de ces congrès qu’est décernée la célèbre médaille Fields. Cantor, endeuillé par la mort de son fils, n’assista pas au premier congrès de 1900. Mais un certain Moritz Cantor y fut présent, sans parenté avec Georg. On pourra consulter le compte rendu de ce congrès numérisé sur mathunion.org (» réf.13). La conférence de Moritz Cantor, Historiographie des mathématiques, débute en page 33. La France hébergea le CIM en 1920 (Strasbourg) et en 1970 (Nice).La théorie des ensembles :

Parue dans le journal de Crelle en 1874, la théorie des ensembles de Cantor, initiée en fait par Dedekind et, dans une certaine mesure, Boole, compte tenu de l’aspect logique liant sa théorie au principe du tiers exclu d’Aristote réalisait le rêve de Leibniz : un langage simple, concis, universel, complété par la logique des prédicats, permettait de formaliser et d’exprimer la pensée mathématique. Mais dès 1889, Cantor rencontre des anomalies dans la théorie des ensembles infinis et des contradictions sont mises en lumière par Burali-Forti (1897), puis Russell (1901).

Georg Cantor (1845-1918)Georg (Ferdinand Ludwig Philipp) Cantor était un mathématicien russo-allemand qui a créé la théorie moderne des ensembles et l’a étendue pour donner le concept de nombres transfinis, avec des classes de nombres cardinaux et ordinaux. Bien que les premiers travaux de Cantor concernent les séries de Fourier, sa réputation repose sur sa contribution à la théorie des ensembles transfinis. Il part de la définition des ensembles infinis proposée par Dedekind en 1872 : un ensemble est infini lorsqu’il est semblable à une partie propre de lui-même. Les ensembles ayant cette propriété, comme l’ensemble des nombres naturels, sont dits « dénombrables » ou « dénombrables ». Sa carrière a été interrompue à plusieurs reprises après 1884 par une maladie mentale. Il mourut d’une insuffisance cardiaque en 1918 dans un établissement psychiatrique.