George Birkhoff était un mathématicien américain formé à Chicago et à Harvard. Il est devenu professeur à Harvard. Son travail le plus important était le théorème ergodique qu’il a découvert en 1931
Le plus grand mathématicien américain du début du XXe siècle. Birkhoff (1884-1944) a fait ses études à l’Université de Chicago, où il a obtenu son doctorat. en 1907. Il a ensuite enseigné à l’Université du Wisconsin (1907-1909), à Princeton (1909-1912) et à Harward (1912-1939). Il a été président de l’American Mathematical Society (1924-26), doyen de la Harvard Faculty of Arts and Sciences (1935-39) et président de l’American Association for the Advancement of Science (1936-37). 
Il a également été rédacteur en chef des Annals of Mathematics (1911-13), des Transactions of the American Mathematical Society (1920-25) et de l’American Journal of Mathematics (1943-44). Au cours de sa carrière, Birkhoff a été honoré de nombreux prix et récompenses. 
Birkhoff a mené des recherches principalement en analyse mathématique et en analyse appliquée à la dynamique. Il a formulé le théorème ergodique, qui a transformé l’hypothèse ergodique de Maxwell-Boltzmann de la théorie cinétique des gaz en un principe rigoureux. Il a également étudié les équations différentielles linéaires et la théorie des équations aux différences. Il a étudié les orbites périodiques et les problèmes à trois corps dans le cadre de la théorie générale des systèmes dynamiques et de la théorie ergodique, et a découvert l’existence d’un nombre infini de solutions périodiques au problème restreint des trois corps. Le monde de la physique d’Éric Weisstein Birkhoff a également étudié la régularisation dans un article de 1915. En topologie, Birkhoff a prouvé le dernier théorème géométrique de Poincaré, un cas particulier du problème des trois corps Le monde de la physique d’Eric Weisstein (1913) et a également fait d’importants travaux sur le théorème des quatre couleurs Le monde des mathématiques d’Eric Weisstein. Il a étudié la mécanique des fluides en relation avec le traitement mathématique de la viscosité. Il a également étudié les fondements de la relativité et de la mécanique quantique, développé une théorie de la gravitation et construit une théorie mathématique de l’esthétique, qu’il a appliquée à l’art, à la musique et à la poésie.
George David Birkhoff et le théorème ergodique
Le 21 mars 1884, le mathématicien américain George David Birkhoff est né. Birkhoff est surtout connu pour ce qu’on appelle aujourd’hui le théorème ergodique. Birkhoff était l’un des leaders les plus importants des mathématiques américaines de sa génération et, à son époque, il était considéré par beaucoup comme le mathématicien américain par excellence. 
« L’importance transcendante de l’amour et de la bonne volonté dans toutes les relations humaines est démontrée par leur puissant effet bienfaisant sur l’individu et sur la société. » –Georges David Birkhoff George David Birkhoff – Petite enfance George David Birkhoff est né à Overisel Township, Michigan, fils de David Birkhoff, médecin, et de Jane Gertrude Droppers. Birkhoff a fréquenté le Lewis Institute (maintenant l’Illinois Institute of Technology) à Chicago de 1896 à 1902. En 1901, il a commencé une correspondance avec Harry Vandiver sur un problème de théorie des nombres. Ensemble, ils ont étudié les facteurs premiers de a n – b n et ont ensuite rédigé leur travail pour publication. Ensuite, il a passé un an à l’Université de Chicago avant de passer à l’Université de Harvarden 1903 (AB, 1905 ; AM, 1906). Pendant son séjour à Harvard, il soumit les résultats qu’il avait obtenus avec Vandiver aux Annals of Mathematics en 1904 et cet article conjoint sur la théorie des nombres devint sa première publication.
L’influence de Poincaré
Il retourna à Chicago en 1905 et y obtint un doctorat en 1907 avec une thèse sur les propriétés asymptotiques de certaines équations différentielles ordinaires avec des applications à la valeur limite et au problème d’expansion. Ses recherches se sont concentrées sur les expansions asymptotiques, les problèmes aux limites et les problèmes de type Sturm-Liouville, mais son directeur de thèse, Eliakim Moore, semble avoir été un guide moins influent pour Birkhoff que ne l’était Poincaré. Birkhoff a lu les travaux de Poincaré sur les équations différentielles et la mécanique céleste et il a appris plus, et a été plus fortement influencé dans la direction que prenait sa recherche, par Poincaré que par son superviseur.
Carrière académique
Birkhoff a enseigné à l’Université du Wisconsin à Madison en tant qu’instructeur de 1907 à 1909. Puis, il est allé à Princeton en tant que précepteur en mathématiques, y devenant professeur en 1911. L’année suivante, il a déménagé à Harvard en tant que professeur adjoint, il a été promu professeur titulaire là-bas en 1919, restant à Harvard pour le reste de sa vie. Coloration du graphique En 1912, en tentant de résoudre le problème des quatre couleurs , c’est-à-dire étant donné toute séparation d’un plan en régions contiguës, produisant une figure appelée carte, il ne faut pas plus de quatre couleurs pour colorer les régions de la carte afin qu’aucune région adjacente n’ait de la même couleur, Birkhoff a introduit le polynôme chromatique , qui compte le nombre de colorations du graphe s en fonction du nombre de couleurs. Même si cette ligne d’attaque ne s’est pas avérée fructueuse, le polynôme lui-même est devenu un objet d’étude important dans la théorie algébrique des graphes.
En 1913, Birkhoff a prouvé le « dernier théorème géométrique » de Poincaré, un cas particulier du problème des trois corps, un résultat qui l’a rendu mondialement célèbre. Le théorème, que Poincaré a annoncé sans preuve en 1912 peu avant sa mort, confirme l’existence d’un nombre infini de solutions périodiques pour le problème restreint des trois corps – c’est-à-dire des orbites stables impliquant trois corps (solaires).[2] Birkhoff a écrit sur les fondements de la relativité et de la mécanique quantique , publiant (avec RE Langer) la monographie Relativity and Modern Physics en 1923. En 1923, Birkhoff a également prouvé que la géométrie de Schwarzschild est l’unique solution à symétrie sphérique des équations du champ d’Einstein. Une conséquence est que les trous noirs ne sont pas simplement une curiosité mathématique, mais pourraient résulter de n’importe quelle étoile sphérique ayant une masse suffisante.
Le théorème ergodique
En 1931, stimulé par les travaux récents de John von Neumann et d’autres, il publie sa formulation du théorème ergodique, qui est probablement devenu son résultat le plus durable. Combinant les connaissances de la physique sur l’hypothèse ergodique avec la théorie de la mesure, ce théorème a résolu, au moins en principe, un problème fondamental de la mécanique statistique. Le théorème ergodique a également eu des répercussions sur la dynamique, la théorie des probabilités, la théorie des groupes et l’analyse fonctionnelle. Il a également travaillé sur la théorie des nombres, le problème de Riemann-Hilbert et le problème des quatre couleurs. Il a proposé une axiomatisation de la géométrie euclidienne différente de celle de Hilbert ; ce travail a abouti à son texte Géométrie de base (1941).
Mesure esthétique et gravitation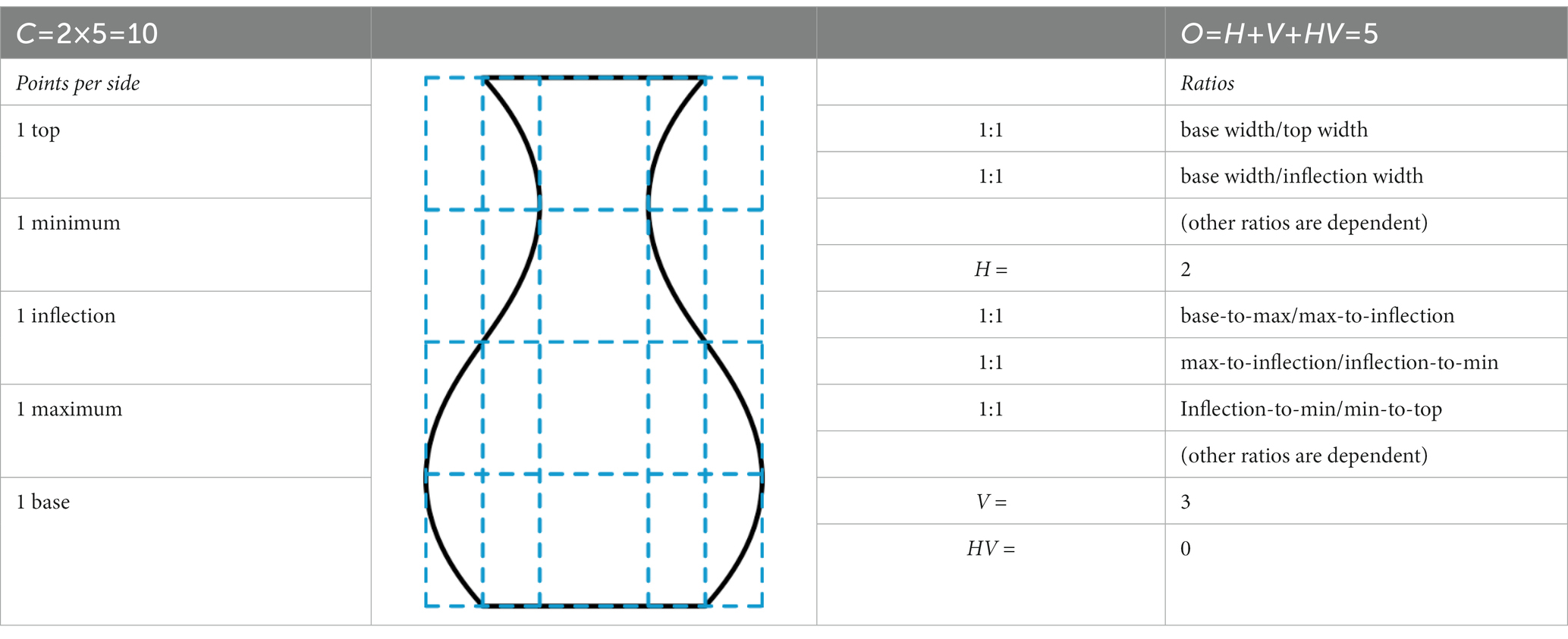
Dans ses dernières années, Birkhoff a publié deux ouvrages curieux. Son Aesthetic Measure de 1933 proposait une théorie mathématique de l’esthétique, pour laquelle il passa un an à étudier l’art, la musique et la poésie de diverses cultures à travers le monde. Son Electricity as a Fluid de 1938 combinait ses idées sur la philosophie et la science. Sa théorie de la gravitation de 1943 est également déroutante, puisque Birkhoff savait que sa théorie n’admet comme sources que la matière qui est un fluide parfait dans lequel la vitesse du son doit être égale à la vitesse de la lumière.
Les fondements de la relativité et de la mécanique quantique étaient également des sujets étudiés par Birkhoff. Conjointement avec RE Langer, il publie la monographie Relativity and Modern Physics en 1923. Vers la fin de sa vie, il publie un ouvrage plus spéculatif, combinant ses idées sur la philosophie et la science, dans Electricity as a Fluid en 1938. Il a également fait un travail important sur le théorème des quatre couleurs. Il a développé une théorie mathématique de l’esthétique qu’il a appliquée à l’art, à la musique et à la poésie. Avant d’écrire Mesure esthétique, il a passé un an à parcourir le monde pour étudier l’art, la musique et la poésie et divers pays.
En 1923, l’American Mathematical Society décerna le premier prix du Bôcher Memorial Prize à Birkhoff pour ses mémoires, Dynamical systems with twodegrees ofliberty, qu’il avait publiés dans les Transactions of the American Mathematical Society en 1917. Il a eu une longue association avec l’American Mathematical Society étant vice-président en 1919, conférencier du colloque en 1920 lorsqu’il a donné des conférences sur les systèmes dynamiques, il a édité les Transactions de l’American Mathematical Society de 1921 à 1924 et a été président de 1925 à 1926. Peut-être que ce haut niveau d’implication avec l’American Mathematical Society suggère déjà que Birkhoff a travaillé sans relâche pour faire progresser les mathématiques en Amérique. En fait Veblena décrit ses efforts dans ce direct comme « une sorte de dévotion religieuse ». Il s’est rendu compte, bien sûr, que faire progresser les mathématiques en Amérique signifiait avoir des contacts étroits avec les progrès dans le reste du monde. Ses contacts étroits avec des mathématiciens en Europe ont fait de lui une personne physique pour rédiger un rapport pour l’International Education Board sur l’état des mathématiques en Europe. Parmi les mathématiciens européens, ses amis les plus proches étaient Hadamard, Niels Nörlund, Levi-Civita et Whittaker.
Un intérêt local à St Andrews est le fait que Birkhoff était l’un des principaux orateurs du colloque de St Andrews de 1926 et a été élu membre honoraire de l’Edinburgh Mathematical Society en 1927. Il a donné quatre conférences lors des célébrations du tricentenaire de Gregory par la Société mathématique d’Édimbourg en juillet 1938 et a reçu un doctorat honorifique en droit par l’Université de St Andrews lors de sa visite en 1938. C’était, en fait, l’un des treize diplômes honorifiques qu’il a reçus. Parmi les autres distinctions que Birkhoff a reçues, citons le prix Querini-Stampalia du Royal Venice Institute of Science en 1917 pour son article Le problème restreint de trois corps publié en 1915, le prix annuel de l’American Association for the Advancement of Science en 1926, et le prix biennal de l’Accademia dei Linceià Rome en 1935. Il a été élu à l’Académie nationale des sciences, à l’American Philosophical Society, à l’Académie américaine des arts et des sciences, à l’Académie des sciences de Paris, à l’Académie pontificale des sciences, au Circolo Matematico di Palermo, à l’Académie royale danoise des sciences et des lettres. , l’Académie de Göttingen, l’Institut royal de Bologne, la Société mathématique d’Édimbourg, la Société mathématique de Londres et l’Académie nationale des sciences de Lima, au Pérou. Il s’agit d’une reconnaissance mondiale remarquable pour la contribution exceptionnelle de Birkhoff.
Des années plus tard
Parmi de nombreux honneurs et récompenses, Birkhoff a été élu à l’Académie nationale des sciences, à l’American Philosophical Society, à l’ American Academy of Arts and Sciences , à l’ Académie des sciences de Paris, à l’Académie pontificale, au Circolo Matematico di Palermo , à l’Académie royale danoise des sciences et des lettres, l’Académie de Göttingen, l’Institut royal de Bologne, la Société mathématique d’Édimbourg, la Société mathématique de Londres et l’Académie nationale des sciences de Lima, au Pérou. George David Birkhoff est décédé le 12 novembre 1944 à Cambridge Massachussetts, à l’âge de 60 ans.
George David Birkhoff (1884-1944)
Mathématicien américain, avant tout du début du XXe siècle, qui a formulé le théorème ergodique. En tant que premier dynamicien américain, Birkhoff a repris là où Poincaré s’était arrêté, se distinguant en 1913 avec sa preuve du dernier théorème géométrique de Poincaré, un cas particulier du problème à 3 corps. Bien qu’avant tout géomètre, il découvre de nouvelles méthodes symboliques. Il a vu au-delà de la théorie des oscillations, a créé une théorie rigoureuse du comportement ergodique et a prévu des modèles dynamiques pour le chaos. Son théorème ergodique a transformé l’hypothèse ergodique de Maxwell-Boltzmann de la théorie cinétique des gaz (à laquelle des exceptions sont connues) en un principe rigoureux grâce à l’utilisation de la théorie des mesures de Lebesgue. Il a également produit un modèle mathématique de la gravité.
https://scienceworld.wolfram.com/biography/Birkhoff.html
https://mathshistory.st-andrews.ac.uk/Biographies/Birkhoff/