
 Brook Taylor était un mathématicien anglais qui a ajouté aux mathématiques une nouvelle branche maintenant appelée le « calcul des différences finies », a inventé l’intégration par parties et a découvert la célèbre formule connue sous le nom d’expansion de Taylor.
Brook Taylor était un mathématicien anglais qui a ajouté aux mathématiques une nouvelle branche maintenant appelée le « calcul des différences finies », a inventé l’intégration par parties et a découvert la célèbre formule connue sous le nom d’expansion de Taylor.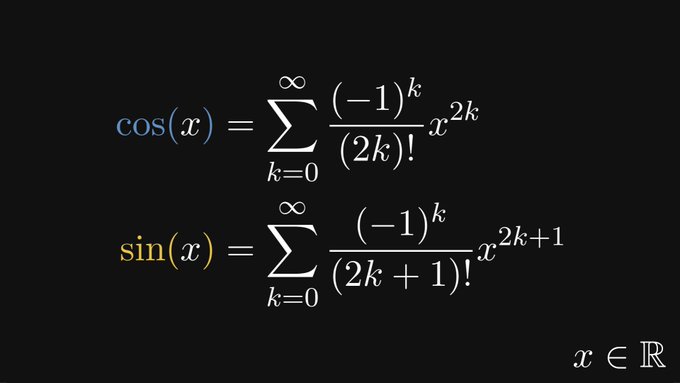
« Il est généralement considéré comme très ridicule de prétendre écrire un poème héroïque ou un beau discours sur n’importe quel sujet, sans comprendre la propriété de la langue dans laquelle il est écrit ; et pour moi, il ne semble pas moins ridicule de prétendre faire une bonne image sans comprendre la perspective… » – Brook Taylor, New Principles of Linear Perspective (1715, 1749) 
Brook Taylor est né à Edmonton de John Taylor de Bifrons House, Kent, et d’Olivia Tempest en 1685. C’était l’année où le roi Charles II est décédé et son frère catholique romain lui a succédé en tant que roi Jacques II d’Angleterre, l’année de la rébellion de Monmouth, dirigée par James Scott, 1er duc de Monmouth, fils illégitime de Charles II. Newton était sur le point de publier sa Philosophiæ Naturalis Principia Mathematica (1687) et celle de Leibniz les écrits mathématiques les plus importants étaient sur le point d’être publiés. Brook Taylor a grandi non seulement pour être un musicien et un peintre accompli , mais il a appliqué ses compétences mathématiques à ces deux domaines plus tard dans sa vie. Il entra au St John’s College, à Cambridge, en tant que compatriote en 1701, et obtint des diplômes de LL.B et LL.D. _ En 1709 et 1714, respectivement. Ayant étudié les mathématiques, il obtint en 1708 une solution remarquable du problème du « centre d’oscillation », qui resta cependant inédite jusqu’en mai 1714, date à laquelle sa prétention à la priorité fut contestée par Johann Bernoulli.
En 1712, Taylor fut élu à la Royal Society et en fut le secrétaire du 13 janvier 1714 au 21 octobre 1718. Il s’agissait clairement d’une élection basée davantage sur l’expertise que ses tuteurs et d’autres savaient que Taylor possédait, plutôt que sur ses résultats publiés. Toujours en 1712, Taylor fut nommé au comité mis en place pour décider si la prétention de Newton ou de Leibniz d’avoir inventé le calcul était correcte.
Le Methodus Incrementorum Directa et Inversa de Taylor (1715) a ajouté une nouvelle branche aux mathématiques supérieures, maintenant appelée le « calcul des différences finies ». Entre autres applications ingénieuses, il l’utilisa pour déterminer la forme du mouvement d’une corde vibrante, par lui d’abord réduite avec succès à des principes mécaniques. Le même ouvrage contenait la célèbre formule connue sous le nom de formule de Taylor, dont l’importance est restée méconnue jusqu’en 1772, lorsque JL Lagrange l’a proclamée le principe de base du calcul différentiel.
Entre 1712 et 1724, Taylor a publié treize articles sur des sujets aussi divers que la description d’expériences sur l’action capillaire, le magnétisme et les thermomètres. Il a rendu compte d’une expérience pour découvrir la loi de l’attraction magnétique (1715) et une méthode améliorée pour approximer les racines d’une équation en donnant une nouvelle méthode pour calculer les logarithmes (1717). Artiste très doué, Taylor a également écrit sur les fondements de la perspective en 1715 et a été le premier à décrire le principe du point de fuite.
Taylor a été marié deux fois. Son mariage en 1721 avec Mlle Brydges de Wallington, Surrey, a conduit à une séparation de son père, qui s’est terminée en 1723 après sa mort en donnant naissance à un fils, qui est également mort. En 1725, il épousa – cette fois avec l’approbation de son père – Sabetta Sawbridge d’Olantigh, Kent, qui mourut également en couches en 1730. Cependant, sa fille, Elizabeth, survécut. La santé fragile de Taylor céda et il tomba dans un déclin, et mourut le 30 novembre 1731, à 46 ans.
« Comme mathématicien, il était le seul Anglais, après Newton et Cotes, capable de tenir tête aux Bernoulli ; mais une grande partie de l’effet de ses démonstrations a été perdue parce qu’il n’a pas exprimé pleinement et clairement ses idées. « 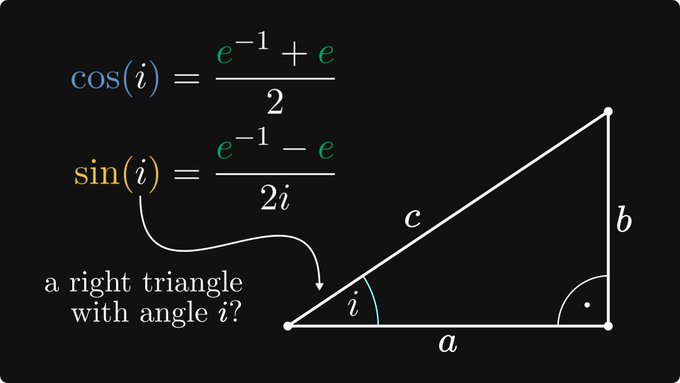

 L’année 1714 marque également l’année où Taylor a été élu secrétaire de la Royal Society. C’était un poste que Taylor a occupé du 14 janvier de cette année jusqu’au 21 octobre 1718lorsqu’il a démissionné, en partie pour des raisons de santé, en partie en raison de son manque d’intérêt pour le poste plutôt exigeant. La période pendant laquelle Taylor était secrétaire de la Royal Society marque ce qui doit être considéré comme sa période la plus productive sur le plan mathématique. Deux livres parus en 1715, Methodus incrementorum directa et inversa et Linear Perspective sont extrêmement importants dans l’histoire des mathématiques. Le premier de ces livres contient ce qui est maintenant connu sous le nom de série Taylor, bien qu’il ne soit connu sous ce nom qu’en 1785. Les deuxièmes éditions paraîtront en 1717 et 1719respectivement. Nous discutons en détail du contenu de ces travaux ci-dessous. Taylor a effectué plusieurs séjours en France. Ceux-ci ont été faits en partie pour des raisons de santé et en partie pour rendre visite aux amis qu’il s’y était fait. Il rencontre Pierre Rémond de Montmort et correspond avec lui sur divers sujets mathématiques après son retour. En particulier, ils ont discuté des séries infinies et des probabilités. Taylor a également correspondu avec de Moivre sur les probabilités et il y avait parfois une discussion à trois entre ces mathématiciens.
L’année 1714 marque également l’année où Taylor a été élu secrétaire de la Royal Society. C’était un poste que Taylor a occupé du 14 janvier de cette année jusqu’au 21 octobre 1718lorsqu’il a démissionné, en partie pour des raisons de santé, en partie en raison de son manque d’intérêt pour le poste plutôt exigeant. La période pendant laquelle Taylor était secrétaire de la Royal Society marque ce qui doit être considéré comme sa période la plus productive sur le plan mathématique. Deux livres parus en 1715, Methodus incrementorum directa et inversa et Linear Perspective sont extrêmement importants dans l’histoire des mathématiques. Le premier de ces livres contient ce qui est maintenant connu sous le nom de série Taylor, bien qu’il ne soit connu sous ce nom qu’en 1785. Les deuxièmes éditions paraîtront en 1717 et 1719respectivement. Nous discutons en détail du contenu de ces travaux ci-dessous. Taylor a effectué plusieurs séjours en France. Ceux-ci ont été faits en partie pour des raisons de santé et en partie pour rendre visite aux amis qu’il s’y était fait. Il rencontre Pierre Rémond de Montmort et correspond avec lui sur divers sujets mathématiques après son retour. En particulier, ils ont discuté des séries infinies et des probabilités. Taylor a également correspondu avec de Moivre sur les probabilités et il y avait parfois une discussion à trois entre ces mathématiciens. Entre 1712 et 1724Taylor a publié treize articles sur des sujets aussi divers que la description d’expériences sur l’action capillaire, le magnétisme et les thermomètres. Il a rendu compte d’une expérience pour découvrir la loi de l’attraction magnétique (1715) et une méthode améliorée pour approximer les racines d’une équation en donnant une nouvelle méthode pour calculer les logarithmes (1717). Sa vie, cependant, a subi une série de tragédies personnelles à partir de 1721 environ. Cette année-là, il épousa Miss Brydges de Wallington dans le Surrey. Bien qu’elle soit issue d’une bonne famille, ce n’était pas une famille avec de l’argent et le père de Taylor s’est fermement opposé au mariage. Le résultat fut que les relations entre Taylor et son père se rompirent et il n’y eut aucun contact entre le père et le fils jusqu’en 1723. C’est cette année-là que la femme de Taylor est décédée en couches. L’enfant, qui aurait été leur premier, est également décédé.
Entre 1712 et 1724Taylor a publié treize articles sur des sujets aussi divers que la description d’expériences sur l’action capillaire, le magnétisme et les thermomètres. Il a rendu compte d’une expérience pour découvrir la loi de l’attraction magnétique (1715) et une méthode améliorée pour approximer les racines d’une équation en donnant une nouvelle méthode pour calculer les logarithmes (1717). Sa vie, cependant, a subi une série de tragédies personnelles à partir de 1721 environ. Cette année-là, il épousa Miss Brydges de Wallington dans le Surrey. Bien qu’elle soit issue d’une bonne famille, ce n’était pas une famille avec de l’argent et le père de Taylor s’est fermement opposé au mariage. Le résultat fut que les relations entre Taylor et son père se rompirent et il n’y eut aucun contact entre le père et le fils jusqu’en 1723. C’est cette année-là que la femme de Taylor est décédée en couches. L’enfant, qui aurait été leur premier, est également décédé.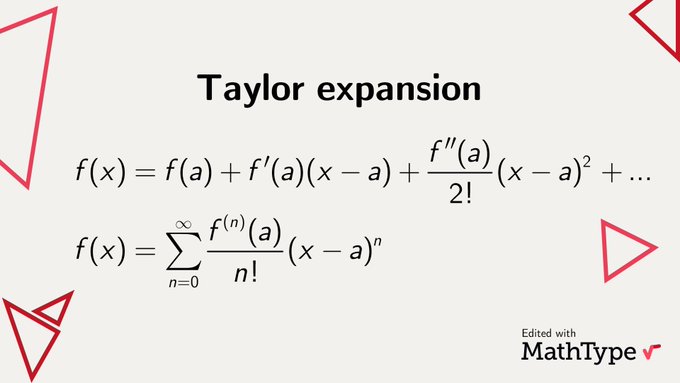
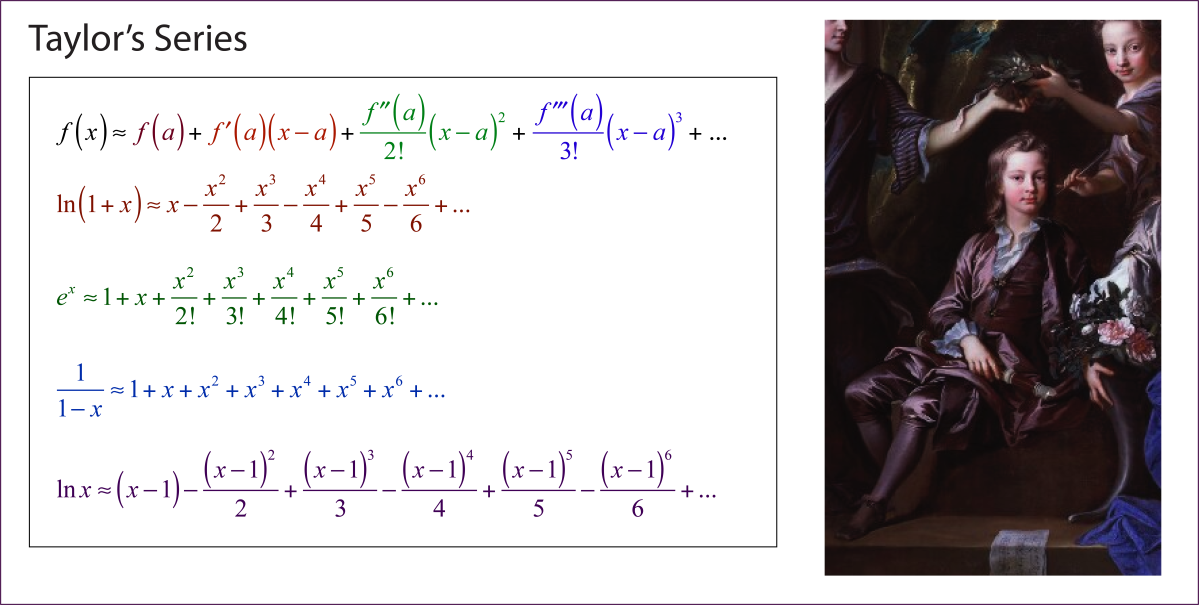 C’était, a écrit Taylor, en raison d’un commentaire que Machin a fait dans Child’s Coffeehouse lorsqu’il avait commenté l’utilisation de « la série de Sir Isaac Newton « , et en utilisant également la « méthode d’extraction des racines du Dr Halley » des équations polynomiales. Il existe, en fait, deux versions du théorème de Taylor données dans l’article de 1715 qui, pour un lecteur moderne, semblent équivalentes mais qui, selon l’auteur de, étaient motivées différemment. Taylor a d’abord dérivé la version qui apparaît comme la proposition 11 comme une généralisation de la méthode de Halley d’approximation des racines de l’équation de Kepler, mais a rapidement découvert que c’était une conséquence de la série de Bernoulli. Il s’agit de la version inspirée de la conversation Coffee house décrite ci-dessus. La deuxième version apparaît comme Corollaire 2à la proposition 7 et a été pensé comme une méthode de développement de solutions d’équations fluxionnelles en séries infinies.
C’était, a écrit Taylor, en raison d’un commentaire que Machin a fait dans Child’s Coffeehouse lorsqu’il avait commenté l’utilisation de « la série de Sir Isaac Newton « , et en utilisant également la « méthode d’extraction des racines du Dr Halley » des équations polynomiales. Il existe, en fait, deux versions du théorème de Taylor données dans l’article de 1715 qui, pour un lecteur moderne, semblent équivalentes mais qui, selon l’auteur de, étaient motivées différemment. Taylor a d’abord dérivé la version qui apparaît comme la proposition 11 comme une généralisation de la méthode de Halley d’approximation des racines de l’équation de Kepler, mais a rapidement découvert que c’était une conséquence de la série de Bernoulli. Il s’agit de la version inspirée de la conversation Coffee house décrite ci-dessus. La deuxième version apparaît comme Corollaire 2à la proposition 7 et a été pensé comme une méthode de développement de solutions d’équations fluxionnelles en séries infinies.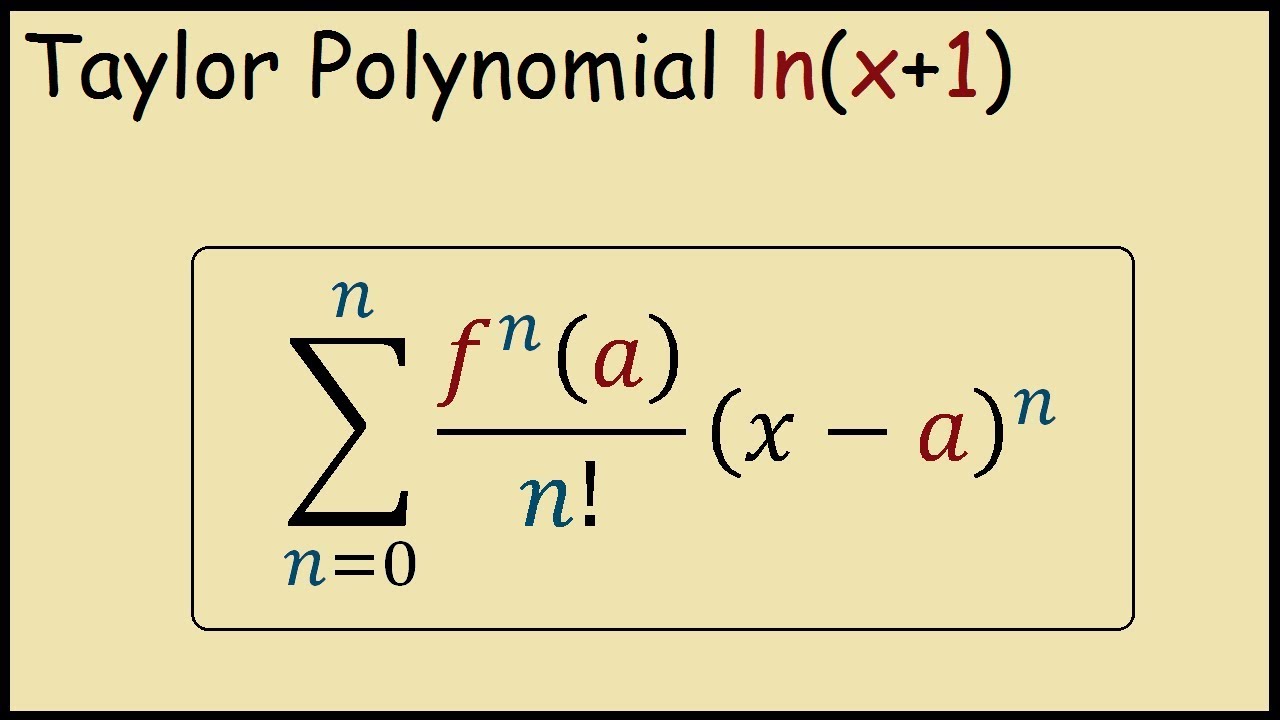 Il y a d’autres idées importantes contenues dans la Methodus incrementorum directa et inversa de 1715 qui n’étaient pas reconnues comme importantes à l’époque. Celles-ci incluent des solutions singulières aux équations différentielles, une formule de changement de variables et une manière de relier la dérivée d’une fonction à la dérivée de la fonction inverse. Il contient également une discussion sur les cordes vibrantes, un intérêt qui vient presque certainement de l’amour précoce de Taylor pour la musique. Taylor, dans ses études sur les cordes vibrantes, n’essayait pas d’établir des équations de mouvement, mais considérait l’oscillation d’une corde flexible en termes d’isochronie du pendule. Il a essayé de trouver la forme de la corde vibrante et la longueur du pendule isochrone plutôt que de trouver ses équations de mouvement.
Il y a d’autres idées importantes contenues dans la Methodus incrementorum directa et inversa de 1715 qui n’étaient pas reconnues comme importantes à l’époque. Celles-ci incluent des solutions singulières aux équations différentielles, une formule de changement de variables et une manière de relier la dérivée d’une fonction à la dérivée de la fonction inverse. Il contient également une discussion sur les cordes vibrantes, un intérêt qui vient presque certainement de l’amour précoce de Taylor pour la musique. Taylor, dans ses études sur les cordes vibrantes, n’essayait pas d’établir des équations de mouvement, mais considérait l’oscillation d’une corde flexible en termes d’isochronie du pendule. Il a essayé de trouver la forme de la corde vibrante et la longueur du pendule isochrone plutôt que de trouver ses équations de mouvement. Taylor a également conçu les principes de base de la perspective dans Linear Perspective (1715). La deuxième édition a un titre différent, s’intitulant Nouveaux principes de la perspective linéaire. L’ouvrage donne un premier traitement général des points de fuite. Taylor avait une approche hautement mathématique du sujet et ne faisait aucune concession aux artistes qui auraient dû trouver les idées d’une importance fondamentale pour eux. Il est parfois très difficile, même pour un mathématicien, de comprendre les résultats de Taylor. L’expression «perspective linéaire» a été inventée par Taylor dans ce travail et il a défini le point de fuite d’une ligne, non parallèle au plan de l’image, comme le point où une ligne à travers l’œil parallèle à la ligne donnée coupe le plan de l’image. Il a également défini la ligne de fuite vers un plan donné, non parallèle au plan de l’image, comme l’intersection du plan passant par l’œil parallèle au plan donné. Il n’a pas inventé les termes point de fuite et ligne de fuite, mais il fut l’un des premiers à en souligner l’importance. Le théorème principal de la théorie de la perspective linéaire de Taylor est que la projection d’une ligne droite non parallèle au plan de l’image passe par son intersection et son point de fuite.
Taylor a également conçu les principes de base de la perspective dans Linear Perspective (1715). La deuxième édition a un titre différent, s’intitulant Nouveaux principes de la perspective linéaire. L’ouvrage donne un premier traitement général des points de fuite. Taylor avait une approche hautement mathématique du sujet et ne faisait aucune concession aux artistes qui auraient dû trouver les idées d’une importance fondamentale pour eux. Il est parfois très difficile, même pour un mathématicien, de comprendre les résultats de Taylor. L’expression «perspective linéaire» a été inventée par Taylor dans ce travail et il a défini le point de fuite d’une ligne, non parallèle au plan de l’image, comme le point où une ligne à travers l’œil parallèle à la ligne donnée coupe le plan de l’image. Il a également défini la ligne de fuite vers un plan donné, non parallèle au plan de l’image, comme l’intersection du plan passant par l’œil parallèle au plan donné. Il n’a pas inventé les termes point de fuite et ligne de fuite, mais il fut l’un des premiers à en souligner l’importance. Le théorème principal de la théorie de la perspective linéaire de Taylor est que la projection d’une ligne droite non parallèle au plan de l’image passe par son intersection et son point de fuite.
Born 338 years ago #Today, Brook Taylor was a mathematician, best known for the eponymous theorem and series, a method for expanding functions into an infinite sum of terms that are expressed as the function's derivatives at a single point https://t.co/krNqu0x1LX pic.twitter.com/UvPlDvOeZ4
— Massimo (@Rainmaker1973) August 18, 2023
La série infinie de Brook Taylor Lorsque Leibniz prétendit en 1704, dans un article publié dans Acta Auditorium, avoir inventé le calcul différentiel en 1684 avant tout le monde, les mathématiciens britanniques se précipitèrent à la défense de Newton. Ils savaient que Newton avait développé ses fluxions dès 1666 et certainement pas plus tard qu’en 1676. Ainsi s’ensuivit l’une des disputes prioritaires les plus amères et partisanes de l’histoire des mathématiques et des sciences qui opposa les Leibniziens continentaux aux Newtoniens insulaires. Bien qu’un comité (partisan) de la Royal Society ait enquêté sur l’affaire et se soit prononcé en faveur de Newton, l’affaire a eu pour effet d’isoler les mathématiques britanniques des mathématiques continentales, créant un désert intellectuel alors que l’avant-garde de l’analyse mathématique se déplaçait vers la France. Seulement quand George Green remplissant ses heures vides des dernières avancées de l’analyse française, tandis qu’il s’occupait du moulin à grain de son père, les mathématiques britanniques se réveillèrent. Green a auto-publié son œuvre épique en 1828 qui a introduit ce qu’on appelle aujourd’hui le théorème de Green.
Lorsque Leibniz prétendit en 1704, dans un article publié dans Acta Auditorium, avoir inventé le calcul différentiel en 1684 avant tout le monde, les mathématiciens britanniques se précipitèrent à la défense de Newton. Ils savaient que Newton avait développé ses fluxions dès 1666 et certainement pas plus tard qu’en 1676. Ainsi s’ensuivit l’une des disputes prioritaires les plus amères et partisanes de l’histoire des mathématiques et des sciences qui opposa les Leibniziens continentaux aux Newtoniens insulaires. Bien qu’un comité (partisan) de la Royal Society ait enquêté sur l’affaire et se soit prononcé en faveur de Newton, l’affaire a eu pour effet d’isoler les mathématiques britanniques des mathématiques continentales, créant un désert intellectuel alors que l’avant-garde de l’analyse mathématique se déplaçait vers la France. Seulement quand George Green remplissant ses heures vides des dernières avancées de l’analyse française, tandis qu’il s’occupait du moulin à grain de son père, les mathématiques britanniques se réveillèrent. Green a auto-publié son œuvre épique en 1828 qui a introduit ce qu’on appelle aujourd’hui le théorème de Green.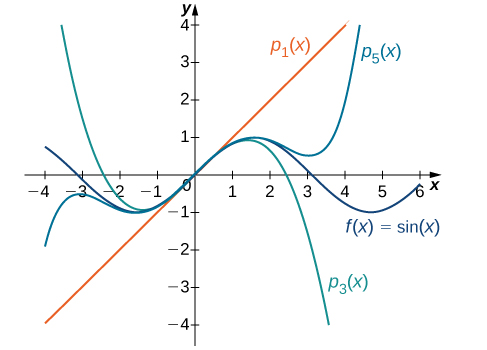 Pourtant, la période de 1700 à 1828 n’était pas un vide complet pour les mathématiques britanniques. Quelques points de lumière brillaient dans l’obscurité, Thomas Simpson, Collin Maclaurin, Abraham de Moivre et Brook Taylor (1685 – 1731) qui venaient d’une famille anglaise qui avait été élevée à la petite noblesse par un acte de Cromwell pendant la guerre anglaise Guerre civile.
Pourtant, la période de 1700 à 1828 n’était pas un vide complet pour les mathématiques britanniques. Quelques points de lumière brillaient dans l’obscurité, Thomas Simpson, Collin Maclaurin, Abraham de Moivre et Brook Taylor (1685 – 1731) qui venaient d’une famille anglaise qui avait été élevée à la petite noblesse par un acte de Cromwell pendant la guerre anglaise Guerre civile.
Grandir à Bifrons House
Lorsque Brook Taylor avait dix ans, son père a acheté Bifrons House [1], l’une des grandes maisons de campagne anglaises, située dans le comté de Kent à seulement un mile au sud de Canterbury. Les maisons de campagne anglaises ont été d’importants centres culturels et sources d’emploi pendant 300 ans, du XVIIe siècle au début du XXe siècle. Bien qu’elles soient généralement les maisons de campagne de la noblesse de tous niveaux, des barons aux ducs, elles appartenaient parfois à des familles riches ou à des représentants au Parlement, ce qui était le cas pour les Taylor. La maison Bifrons avait été construite vers 1610 dans le style architectural jacobéen qui était populaire sous le règne de James I. La maison avait une façade majestueuse, avec des tours carrées surmontées d’une coupole, des pignons sur le toit, des porches de forme renaissance et de vastes jardins bien entretenus du côté sud. Bifrons House est resté le siège de la famille Taylor jusqu’en 1824, date à laquelle ils ont déménagé dans une maison plus grande à proximité et ont d’abord laissé Bifrons à un marquis, puis en 1828 à Lady Byron (ex-épouse de Lord Byron) et sa fille Ada Lovelace (la célèbre mathématicienne pour ses contributions aux débuts de l’informatique). Les Taylor ont vendu la maison en 1830 au premier marquis Conyngham.
La vie de Taylor grandissant dans l’environnement raréfié de Bifrons House a dû ressembler à des scènes du drame télévisé populaire de la BBC Downton Abbey. La maison avait un grand nombre de serviteurs et un grand terrain au bord d’un grand parc près de la ville de Patrixbourne. La vie en tant qu’héritier du domaine aurait été remplie d’événements sociaux et de beaux-arts qui comprenaient la musique et la peinture. Taylor a développé un amour de la musique tout au long de sa vie pendant son enfance, collaborant plus tard avec Isaac Newton sur une enquête scientifique sur la musique (elle n’a jamais été publiée). Il était également un artiste amateur, et l’un des premiers livres qu’il a publiés après avoir été élu à la Royal Society était sur les mathématiques de la perspective linéaire, qui contenait certains des premiers résultats de la géométrie projective.
Il y a un beau portrait de famille à la National Portrait Gallery de Londres peint par John Closterman vers 1696. Le portrait est celui des enfants de John Taylor environ un an après avoir acheté Bifrons House. Le tableau est remarquable car Brook, l’héritier de la fortune familiale, est couronné d’une couronne par ses deux sœurs aînées (qui n’hériteraient pas). Brook n’avait qu’environ 11 ans à l’époque et était déjà célèbre au sein de sa famille pour ses capacités avec la musique et les chiffres.
Taylor n’a jamais eu à aller à l’école, étant complètement tutoré à la maison jusqu’à ce qu’il entre au St.John’s College de Cambridge, en 1701. Il suivit des cours de mathématiques à Machin et Keill et obtint son diplôme en 1709. L’allocation de son père était suffisant pour lui permettre de mener la vie d’un gentleman érudit, et il fut élu membre de la Royal Society en 1712 et élu secrétaire de la Société à peine deux ans plus tard. Au cours des années suivantes, il fut actif en tant que mathématicien montant jusqu’en 1721, date à laquelle il épousa une femme de bonne famille mais sans richesse. Le soutien d’une maison comme Bifrons prenait toujours de l’argent, et le manque d’argent de la nouvelle épouse suffisait au père de Taylor pour expulser le nouveau couple. Malheureusement, sa femme mourut en couches avec l’enfant, alors Taylor rentra chez lui en 1723. Ces problèmes familiaux mit fin à ses principales années de productivité en tant que mathématicien.
Méthode incrémentale directe et inverse  Sous l’œil du mathématicien newtonien Keill à Cambridge, Taylor est devenu un fervent partisan et utilisateur des fluxions de Newton. Juste après avoir été élu membre de la Royal Society en 1712, il participa à une enquête sur la priorité de l’invention du calcul qui opposait les newtoniens britanniques aux leibniziens continentaux. La Royal Society s’est prononcée en faveur de Newton (évidemment) et a évoqué la possibilité que Leibniz ait appris les idées de Newton lors d’une visite en Angleterre quelques années seulement avant que Leibniz ne développe sa propre version du calcul différentiel.
Sous l’œil du mathématicien newtonien Keill à Cambridge, Taylor est devenu un fervent partisan et utilisateur des fluxions de Newton. Juste après avoir été élu membre de la Royal Society en 1712, il participa à une enquête sur la priorité de l’invention du calcul qui opposait les newtoniens britanniques aux leibniziens continentaux. La Royal Society s’est prononcée en faveur de Newton (évidemment) et a évoqué la possibilité que Leibniz ait appris les idées de Newton lors d’une visite en Angleterre quelques années seulement avant que Leibniz ne développe sa propre version du calcul différentiel. 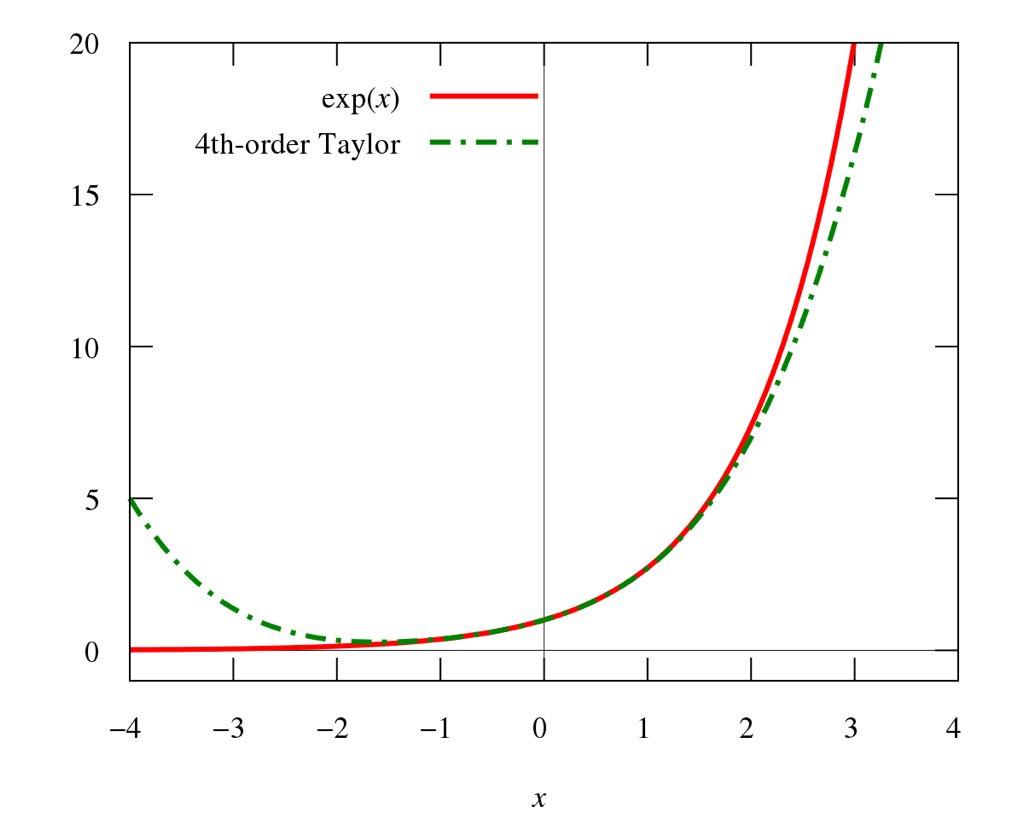
Une fois que Taylor a été initié aux fluxions de Newton, il s’est accroché et a aidé à pousser son développement. La même année (1715) qu’il publie un livre sur la perspective linéaire pour l’art, il publie également un livre révolutionnaire sur l’utilisation du calcul pour résoudre des problèmes pratiques. Ce livre, Methodus incrementorum directa et inversa, a introduit plusieurs nouvelles idées, y compris les méthodes de différences finies (qui sont couramment utilisées aujourd’hui dans les simulations numériques d’équations différentielles). Il a également examiné pour la première fois les solutions possibles à l’équation d’une corde vibrante.
La corde vibrante est l’un des problèmes les plus simples de la « mécanique du continuum », mais elle a posé un sérieux défi à la physique newtonienne des particules ponctuelles. Ce n’est que beaucoup plus tard que D’Alembert a utilisé la première loi d’action-réaction de Newton pour éliminer les forces internes pour dériver le principe de D’Alembert sur la force nette sur un corps étendu. Pourtant, Taylor a utilisé des différences finies pour traiter la masse linéaire de la corde d’une manière qui a donné une solution possible d’une fonction sinusoïdale. Taylor a été le premier à proposer qu’une fonction sinusoïdale était la forme du déplacement de la corde pendant la vibration. Cette idée sera reprise plus tard par D’Alembert (qui a d’abord dérivé l’équation d’onde), et par Euler (qui était en désaccord avec véhémence avec les solutions de D’Alembert) et Daniel Bernoulli (qui a été le premier à suggérer qu’il ne s’agit pas d’une seule fonction sinus, mais une somme de fonctions sinus, Bien sûr, l’idée la plus influente du livre de Taylor de 1715 était son utilisation générale d’une série infinie pour décrire une courbe.
Série de Taylor
Les séries infinies sont devenues un nouvel outil majeur dans la boîte à outils d’analyse avec la publication de John Wallis Arithmetica Infinitorum publié en 1656. Peu de temps après, de nombreuses séries ont été publiées telles que la série de Nikolaus Mercator (1668)
Contribution aux mathématiques 
Brook Taylor (1685-1731)
Mathématicien britannique, surtout connu pour la série de Taylor, une méthode pour étendre les fonctions en séries infinies. En 1708, Taylor propose une solution au problème du centre d’oscillation. Son Methodus incrementorum directa et inversa («Méthodes directes et indirectes d’incrémentation», 1715) a introduit ce qu’on appelle maintenant le calcul des différences finies. Grâce à cela, il fut le premier à exprimer mathématiquement le mouvement d’une corde vibrante sur la base de principes mécaniques. Methodus contenait également le théorème de Taylor, reconnu plus tard (1772) par Joseph Lagrange comme la base du calcul différentiel. Artiste doué, Taylor a également écrit sur les principes de base de la perspective (1715) contenant le premier traitement général du principe des points de fuite.
https://galileo-unbound.blog/2020/08/03/brook-taylors-infinite-series/
https://mathshistory.st-andrews.ac.uk/Biographies/Taylor/
https://famous-mathematicians.com/brook-taylor/



