Le guide complet de la logique booléenne
George Boole (1815-1864), est un logicien, mathématicien et philosophe britannique. Il est le créateur de la logique moderne, fondée sur une structure algébrique et sémantique, que l’on appelle algèbre de Boole en son honneur. Il a aussi travaillé dans d’autres domaines mathématiques, des équations différentielles aux probabilités en passant par l’analyse. Autodidacte, il publia ses premiers travaux d’algèbre tout en exerçant son métier d’instituteur et de directeur d’école dans la région de Lincoln.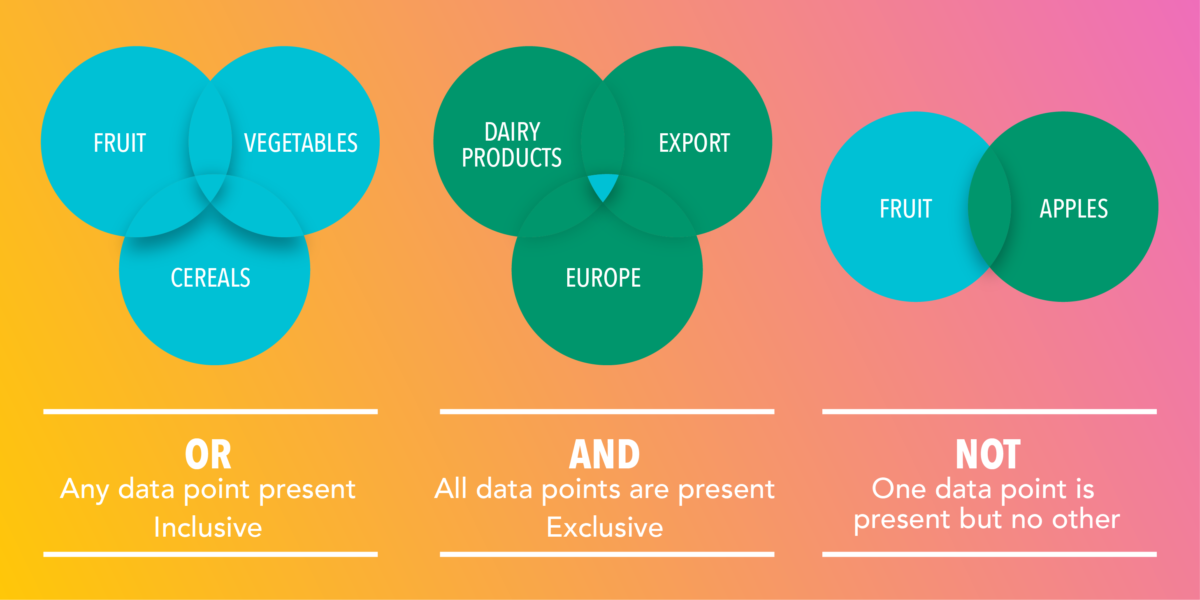
Ses travaux lui valurent en 1844 la Royal Medal de la Royal Society, puis une chaire de mathématiques à l’université (Queen’s College) de Cork en 1849. Boole mène ses travaux les plus importants dans les années 1850 sur les fondements des mathématiques : en 1854 paraît Une enquête sur les lois de la pensée, sur lesquelles sont fondées les théories mathématiques de la logique et des probabilités. Boole approche la logique par un calcul purement algébrique nommé depuis calcul booléen. Cette vision très abstraite est ultérieurement exploitée par Peirce, Frege, Russell, Turing et Shannon, elle est devenue un élément fondamental dans la conception des ordinateurs.
George Boole – Biographie complète, histoire et inventions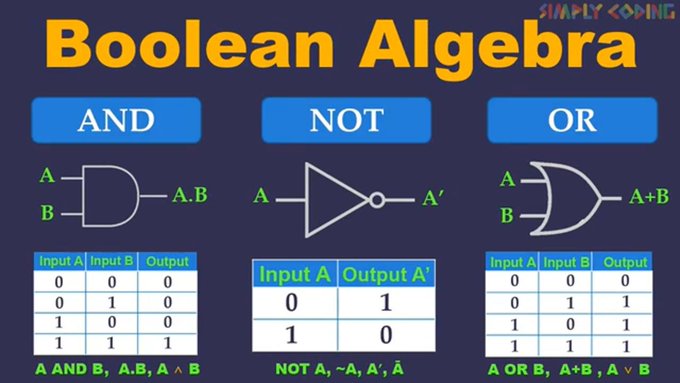
Boole a créé l’algèbre booléenne et ce qu’on appelle la logique booléenne, qui est une théorie à la base des ordinateurs modernes.
La logique booléenne se concentre sur les variables binaires : vrai et faux (également des 1 et des 0).
Qui était George Boole ? 
George Boole était un mathématicien, philosophe et logicien autodidacte. La majeure partie de sa vie professionnelle s’est déroulée en tant que professeur de mathématiques au Queen’s College de Cork en Irlande. Boole a travaillé dans les domaines des équations différentielles et de la logique algébrique. Il est surtout connu pour son livre, The Laws of Thought , publié en 1854. The Laws of Thought contient des informations sur l’algèbre booléenne. La logique booléenne est connue pour avoir jeté les bases de l’ère de l’information. 
Début de la vie
George Boole est né à Lincoln, dans le Lincolnshire, en Angleterre. Ses parents étaient John Boole senior et Mary Ann Joyce. Boole avait une éducation primaire, et plus tard, il a été scolarisé à la maison par son père en raison de leur déclin dans les affaires. Il a peu d’éducation formelle et académique, et était autodidacte en langues modernes. À 16 ans, Boole est devenu professeur junior à l’école Doncaster de Heigham. C’est alors que Boole est devenu le soutien financier de ses parents et de ses jeunes frères et sœurs. Boole a également participé au Lincoln Mechanics Institute, fondé en 1933. C’est alors qu’Edward Bromhead a aidé George Boole en mathématiques. Ensuite, le révérend George Stevens Dickson de St Swithin’s, Lincoln a donné à Boole le texte de calcul de Sylvestre François Lacroix. Malheureusement, Boole n’avait pas de professeur approprié et il lui a fallu de nombreuses années pour maîtriser le calcul. À 19 ans, George Boole a créé sa propre école à Lincoln – Free School Lane. Quatre ans plus tard, après la mort de Robert Hall, Boole a repris la Hall’s Academy à Waddington. En 1840, il retourna à Lincoln, où il dirigea un pensionnat. 
Boole a été impliqué dans la société Lincoln Topographical et a été membre du comité. Boole est devenu une personnalité locale influente et admiré John Kaye, un homme d’église anglais. Plus tard, il a rejoint la campagne locale pour la fermeture anticipée. Il a été formé pour contrôler les heures de travail dans les magasins de détail et mettre fin au commerce du dimanche. À partir de 1838, Boole se met en réseau avec des mathématiciens universitaires britanniques sympathiques et lit plus largement. En outre, Boole a étudié l’algèbre sous la forme de méthodes symboliques et a commencé à publier des articles de recherche.
En 1849, le statut de Boole en tant que mathématicien fut reconnu lorsqu’il fut nommé premier professeur de mathématiques au Queen’s College de Cork en Irlande.
Pourquoi George Boole est-il connu ? 
George Boole : mariage, divorce, enfants et vie personnelle
En 1855, Boole épousa Mary Everest, qui écrivit plus tard plusieurs ouvrages éducatifs sur les principes de Boole. Ils se sont rencontrés en 1850 alors qu’elle rendait visite à son oncle, John Ryall, qui était professeur de grec au Queen’s College de Cork en Irlande. Mary et George ont eu 5 filles : Mary, Margaret, Alicia, Lucy et Ethel.
La tragédie
En novembre 1864, Boole a parcouru trois miles de son domicile à l’université sous de fortes pluies, puis il a donné des conférences dans des vêtements mouillés. Immédiatement, Boole est tombé malade et a développé une pneumonie. Mary, sa femme, croyait qu’elle devait l’envelopper dans des couvertures humides pour le guérir. Son état s’est aggravé et Boole est décédé le 8 décembre 1864 des suites d’un épanchement pleural provoqué par la fièvre. Boole a été enterré dans le cimetière de l’Église d’Irlande de St. Michael’s, Church Road, Blackrock. Une plaque commémorative se trouve à l’intérieur de l’église attenante.
George Boole : Récompenses et réalisations Prix d’or de la Royal Society en mathématiques 
George Boole a remporté le premier prix d’or de mathématiques décerné par la Royal Society en 1844 pour son article «On a General Method in Analysis».
Médaille Keith de la Société royale 
Il a reçu la médaille Keith de la Royal Society of Edinburgh en 1855. Deux ans plus tard, Boole a été élu Fellow de la Royal Society (FRS). Boole a reçu des diplômes honorifiques de LL.D de l’Université de Dublin et de l’Université d’Oxford.
Un support de formation avec des capteurs, des commutateurs et un circuit d’éléments logiques utilisés dans la formation des étudiants pour illustrer la logique booléenne. La logique booléenne est une sous-section de l’algèbre qui décrit un ensemble de règles et de portes simples pour aider à comparer et à manipuler des instructions logiques.
Œuvres et livres publiés de George Boole 
Le premier article publié par Boole était « Recherches sur la théorie des transformations analytiques, avec une application spéciale à la réduction de l’équation générale du second ordre ». Il a été imprimé dans le Cambridge Mathematical Journal en février 1840. Cet article a conduit à une amitié entre Boole et le rédacteur en chef du journal, Duncan Farquharson Gregory. Boole a publié un article influent sur la théorie des invariants précoces en 1841. En 1844, il reçut une médaille de la Royal Society pour ses mémoires, « On a General Method in Analysis. » C’était une contribution à la théorie des équations différentielles linéaires, passant du cas des coefficients constants aux coefficients variables. L’innovation dans les méthodes opérationnelles est d’admettre que les opérations ne peuvent pas faire la navette. Boole a publié « The Mathematical Analysis of Logic » en 1847. Ce fut son premier ouvrage sur la logique symbolique.
Équations différentielles
En 1859 et 1860, Boole publie deux traités systématiques sur des sujets mathématiques. D’abord, « Traité sur les équations différentielles », puis « Traité sur le calcul des différences finies ».
L’identité de Boole
Boole a publié le traité « Sur la comparaison du transcendant, avec certaines applications à la théorie des intégrales définies » en 1857. Dans le traité, il a étudié la somme des résidus d’une fonction rationnelle où il a prouvé ce que nous appelons maintenant : l’identité de Boole – pour n’importe quel nombre réel. Il existe des généralisations de cette identité qui jouent un rôle important dans la théorie de la transformée de Hilbert.
Logique symbolique
En 1847, Boole a publié une brochure intitulée « Analyse mathématique de la logique », plus tard, il voulait que « Une enquête sur les lois de la pensée sur lesquelles sont fondées les théories mathématiques de la logique et des probabilités » soit considérée comme l’énoncé mûr de ses vues. On croyait que Boole n’était pas d’accord avec la logique d’Aristote ; cependant, Boole avait seulement l’intention de le systématiser. Il voulait lui donner un fondement et étendre son champ d’application. Boole s’est d’abord impliqué dans la logique lors d’un débat sur la quantification entre Sir William Hamilton et Augustus De Morgan.
Ce débat a conduit Boole à fonder ce qui fut d’abord connu sous le nom de tradition de «l’algèbre de la logique». Boole avait de nombreuses innovations de son principe de référence holistique, et il a ensuite été adopté par Gottlob Frege et d’autres logiciens qui croyaient en la logique standard du premier ordre. En 2003, un article a été publié qui fournit une comparaison et une évaluation critique entre la logique aristotélicienne et la logique booléenne – il révèle la centralité de la référence holistique dans la philosophie de la logique de Boole.
Théorie des probabilités 
Le guide complet de la logique booléenne
Points clés :
La logique booléenne se concentre strictement sur les variables binaires qui se présentent généralement sous la forme de 1 et de 0, qui représentent « vrai » ou « faux ».
Là où l’algèbre standard manipule les nombres en utilisant l’addition, la soustraction, la multiplication, la division, etc., l’algèbre booléenne utilise des fonctions logiques comme la négation, la conjonction et la disjonction.
La porte la plus simple imaginable s’appelle une porte NON ou un inverseur. Il inverse simplement l’entrée que vous lui donnez pour produire le contraire en sortie.
Qu’est-ce que la logique booléenne ? – Explication complète
La logique booléenne est une sous-section de l’algèbre qui décrit un ensemble de règles et de portes simples pour aider à comparer et à manipuler des instructions logiques. Ce qui distingue la logique booléenne des autres systèmes logiques, c’est qu’elle se concentre strictement sur les variables binaires, qui se présentent généralement sous la forme de 1 et de 0 représentant vrai et faux. Là où l’algèbre régulière couvre les opérations numériques, l’algèbre booléenne s’attaque aux opérations logiques. L’algèbre régulière manipule les nombres en utilisant l’addition, la soustraction, la multiplication, la division et d’autres fonctions mathématiques. L’algèbre booléenne manœuvre ses sujets en utilisant des fonctions logiques comme la négation, la conjonction et la disjonction. Les deux systèmes utilisent les mêmes opérateurs relationnels que les mathématiques classiques, y compris les symboles égal à (=), supérieur à (>) et inférieur à.
L’algèbre ordinaire et la logique booléenne suivent bon nombre des mêmes règles de base. Ceux-ci inclus :
Les lois commutatives, qui vous permettent d’échanger les positions de vos variables lors de l’addition et de la multiplication
Les lois associatives, qui vous permettent de changer l’ordre des opérations lors de l’addition et de la multiplication
Les lois distributives, qui vous permettent de répartir les opérations de multiplication sur les opérations d’addition
Ces règles et quelques autres règles et portes simples pour la manipulation logique nous permettent de mapper une quantité surprenante d’idées et d’énoncés directement sur des bits et des octets numériques. La logique booléenne est aujourd’hui l’épine dorsale de la plupart des langages de programmation informatique. Dans le monde de la finance, il est utilisé par les investisseurs pour évaluer les options et les risques. Il fournit également un moyen simple d’affiner les recherches dans de grandes bases de données d’informations.
Logique booléenne : une définition exacte
La logique booléenne est un système utilisé pour analyser la valeur de vérité de toute instruction binaire, ainsi que les relations entre des ensembles d’instructions binaires, en utilisant des règles algébriques combinées à des portes logiques pour exécuter des opérations logiques.
Comment fonctionne la logique booléenne ?
La logique booléenne commence par des fonctions mathématiques typiques et en ajoute quelques-unes. Les idées principales de la logique booléenne tournent autour de trois portes logiques simples ainsi que de quelques portes plus avancées. Vous pouvez combiner ces portes avec les opérateurs relationnels mathématiques standards et les règles algébriques de base pour construire des arbres d’idées ramifiés que vous pouvez implémenter sur n’importe quel système numérique binaire.
Les trois portes logiques les plus simples comprennent : NE PAS ET OU
NE PAS La porte la plus simple imaginable s’appelle une porte NON ou un onduleur. Tout ce qu’il fait est d’inverser l’entrée que vous lui donnez pour produire le contraire en sortie. Dans un système numérique basé sur des variables binaires de 1 et de 0, l’entrée d’un 1 dans une porte NOT produira un 0 et vice versa. Nous appelons cette fonction logique la porte NOT car l’état d’entrée n’est pas le même que l’état de sortie. Pour désigner cette opération d’inversion, la plupart des définitions de la logique booléenne utilisent un soulignement, qui est une simple barre sur le symbole d’entrée donné (¯). Par exemple, si nous utilisons X pour signifier qu’un interrupteur est fermé, alors « PAS X », ou X avec un surlignement au-dessus, signifie que l’interrupteur est ouvert. En logique booléenne, la porte NOT n’a qu’une seule entrée et une seule sortie. Deux portes NOT connectées dos à dos produisent une double inversion, qui vous rendra votre variable avec sa valeur d’origine.
ET
La porte ET ne produira une action de sortie que si toutes les instructions ou variables qui lui sont connectées sont présentes simultanément. La sortie d’une porte ET ne sera vraie que lorsque toutes les variables jointes par la porte ET seront vraies. Si l’un d’eux est faux, la sortie sera fausse. La porte ET est similaire à l’addition en ce sens qu’elle suit les règles simples de la commutation, permettant à toute variable qu’elle connecte de changer de position. L’un des exemples les plus simples est « X AND Y = Y AND X ». L’ordre des variables n’affecte pas le résultat final et est donc considéré comme sans importance. Nous représentons généralement la porte ET avec un point ou un point (.). Une porte ET avec deux entrées de X et Y se traduit par l’expression booléenne « XY », que de nombreux langages de programmation simplifient en « XY ».
OU
Le porte OU booléen produit une sortie si l’une des variables qu’elle connecte est présente. L’action de sortie de ce type de porte aura une valeur vraie si une ou plusieurs de ses entrées sont vraies. Dans le monde de l’électronique, une porte OU est connue sous le nom de circuit parallèle. Tout comme la porte ET, la porte OU a des propriétés commutatives, permettant à l’une de ses variables d’entrée de changer d’ordre sans affecter la sortie. Le nom complet de la porte OU est en fait « OU inclusif », ce qui le contraste avec une porte logique booléenne plus complexe, « OU exclusif » (XOR). Une porte XOR remplit la fonction opposée, excluant toutes ses entrées et ne produisant une sortie que si aucune d’entre elles n’est présente. Contre-intuitivement, le symbole que nous utilisons pour une porte OU est le signe plus (+). Une porte OU avec deux entrées de X et Y peut être représentée par l’expression booléenne « X + Y ».
Portes logiques plus avancées
Si nous allons un niveau plus loin dans notre système de logique booléenne, nous obtenons des portes logiques plus avancées. Ce ne sont essentiellement que des combinaisons des trois portes les plus simples. Voici quelques-uns des plus importants.
NAND
La porte NAND combine deux des portes logiques simples, la porte NOT et la porte AND, pour former une fonction NOT AND. NAND est un complément de AND, comme vous pouvez le deviner, effectuant l’inversion exacte des règles de la porte AND. La sortie d’une porte NAND ne sera fausse que si toutes les entrées qui s’y connectent sont vraies. Si une ou plusieurs de ses entrées sont fausses, la sortie sera vraie. Le symbole que nous utilisons pour représenter NAND est parfois appelé le trait de Sheffer. Il ressemble à une flèche pointant vers le haut (↑) mais est parfois simplifié en une simple ligne verticale (|). Des exemples d’expressions booléennes impliquant des portes NAND pour joindre les variables X et Y incluent « X↑Y » et « X|Y ».
NI
La porte NOR connecte deux portes logiques simples, NOT et OR, pour créer une fonction NOT OR. Cela agit exactement comme une simple porte OU avec sa sortie inversée. La porte NOR ne vous donnera une sortie que lorsqu’aucune de ses variables n’est présente. La variable de sortie n’aura une valeur vraie que si toutes ses variables d’entrée sont fausses. Il existe deux symboles que nous pouvons utiliser pour une porte NOR. Le premier combine les symboles des portes NON et OU. En utilisant les variables X et Y, cela ressemblera à « X + Y » avec un surlignement en haut. Le second est un symbole plus simplifié connu sous le nom de flèche de Peirce, qui ressemble à une flèche vers le bas (↓). Lorsque vous joignez nos deux variables préférées, cela ressemble à « X↓Y ».
Comment créer une expression booléenne ?
Les expressions booléennes sont la façon dont les langages de programmation comme Java, C et Python implémentent la logique booléenne. Par définition, une expression booléenne doit être une simple déclaration logique qui peut être représentée comme vraie ou fausse. Vous pouvez utiliser ces expressions pour comparer n’importe quel type de données tant que vous entrez le même type de données dans toutes les parties de toutes les expressions. Ils peuvent agir comme une sorte de calculatrice logique pour tester des déclarations et d’autres entrées de données et vérifier si elles sont égales, inférieures ou supérieures à d’autres déclarations ou données. Les expressions booléennes simples nécessitent au moins trois parties : le premier élément que vous souhaitez comparer, la porte ou l’opérateur de comparaison que vous souhaitez effectuer et le deuxième élément à comparer. Vous pouvez également créer des expressions booléennes plus alambiquées en joignant n’importe quelle expression simple à n’importe quelle autre en utilisant NOT, OR, AND, NAND, NOR ou d’autres portes logiques. Assurez-vous que toute expression que vous connectez est une expression booléenne complète en elle-même. Cela peut signifier que vous devez spécifier la même variable à plusieurs endroits.
D’où vient la logique booléenne ? 
Les origines de la logique booléenne remontent à un livre publié en 1854 par George Boole, mathématicien et philosophe. Boole était un jeune Anglais tranquille avec des parents de la classe ouvrière. Sa connaissance des mathématiques était principalement autodidacte. À l’âge de 34 ans, il a fini par devenir le premier professeur de mathématiques d’Irlande dans le premier collège laïc du pays, le Queen’s College. Boole a présenté ses concepts logiques dans son premier livre, « L’analyse mathématique de la logique », et les a approfondis dans une publication ultérieure, « Une enquête sur les lois de la pensée ». Ces livres ont été parmi les premiers à explorer sérieusement l’idée de logique et sa relation avec les mathématiques. 
Dans ceux-ci, il a soutenu qu’au lieu d’être une sorte de philosophie, la logique pouvait être classée comme une discipline mathématique qui pouvait fournir des résultats à des problèmes logiques aussi précisément qu’une calculatrice résolvait des problèmes mathématiques. Il avait remarqué qu’il y avait de nombreuses similitudes profondes entre les symboles et les règles algébriques et les syllogismes et les formes logiques que nous utilisons dans notre tête lorsque nous raisonnons. Il a commencé un voyage ambitieux pour essayer de concevoir un système logique basé sur l’algèbre qui modéliserait notre façon de penser. Boole a passé des années à développer ses idées sur la façon d’encoder des arguments logiques faits naturellement par le cerveau humain dans un langage mathématique. La logique booléenne est l’algèbre linguistique qu’il a inventée.
En 1864, Boole meurt à seulement 49 ans. Son travail est resté pendant des années sans beaucoup d’applications pratiques jusqu’à ce qu’un ingénieur électricien et mathématicien américain du nom de Claude Shannon lui donne vie 70 ans après la mort de Boole. Shannon a reconnu que la logique symbolique de Boole pouvait être utilisée dans des circuits de relais électromécaniques pour former la base de mécanismes de résolution de problèmes du monde réel, ou comme nous les appelons aujourd’hui, des ordinateurs. Avec le recul, de nombreux historiens considèrent George Boole comme l’un des ancêtres de l’informatique. Ses contributions aux structures conceptuelles des circuits numériques modernes et des langages de programmation lui ont valu le mérite bien mérité d’être l’un des fondateurs les plus importants de l’ère de l’information.
Quelles sont les applications de la logique booléenne ?
L’idée de base sous-jacente à tous les ordinateurs numériques d’aujourd’hui est que les commutateurs électriques binaires peuvent être utilisés pour traiter la logique. Ce qui a commencé comme une lueur dans l’œil de George Boole est devenu la base concrète derrière la conception de tous les circuits numériques et le fil de terre conceptuel de l’ère informatique.
Calculatrices aux processeurs
Si nous utilisons différents niveaux de tension pour symboliser les bits binaires, nous pouvons transformer des portes booléennes extrêmement basiques en composants nécessaires pour fabriquer des calculatrices mécaniques simples , y compris des compteurs, des additionneurs et d’autres outils mathématiques. À partir de là, il n’y a qu’un petit pas pour concevoir des circuits qui utilisent la logique booléenne pour soustraire, multiplier, diviser, etc. Comme il n’y a pas si longtemps, les Homo sapiens étaient les seules machines capables de faire des calculs conceptuels, cela en soi est un gros problème. Une fois que nous avons utilisé ces circuits et leurs concepts booléens pour fabriquer une calculatrice de poche, un processeur complet n’est pas trop loin.
Mémoire vive
Une autre chose utile que vous pouvez créer avec les portes logiques booléennes est l’idée de mémoire. Le concept de mémoire repose sur la rétroaction. Lorsque la sortie d’une porte est réinjectée dans son entrée, vous obtenez une mémoire. Tout ce que vous avez à faire pour que les portes logiques booléennes se souviennent d’une valeur d’entrée est de les organiser correctement. Ce concept d’une simplicité embarrassante est ce qui nous donne la mémoire vive (RAM) de nos ordinateurs.
Exemples de logique booléenne dans le monde réel
Dans ta tête
Votre cerveau utilise la logique booléenne tous les jours. Nous appelons les concepts booléens dans nos têtes « conditionnels ». L’idée de brancher des arbres de décision qui dépendent de certaines conditions est un outil important que nous utilisons pour penser clairement.
Voici quelques exemples de la logique booléenne que vous pourriez rencontrer dans votre esprit :
Si j’éternue et que je suis dans une pièce poussiéreuse, ça va. Si j’éternue ou tousse et que j’ai de la fièvre, allez chez le médecin.
Si j’ai soif, bois quelque chose. Si j’ai soif et faim, commandez des boissons et un repas. Si je n’ai ni soif ni faim, je vais me coucher. En recherche et en recherche
Vous pouvez utiliser des termes booléens dans la recherche. Ils peuvent vous aider à affiner ou à élargir la portée de votre recherche lorsque vous parcourez des bases de données ou des catalogues de bibliothèques. La logique booléenne peut également vous aider à améliorer vos recherches sur le Web. Le terme booléen ET vous permet de cibler votre recherche pour rechercher des résultats plus spécifiques. ET affinera votre recherche. Le terme booléen OU vous permet d’inclure des concepts connexes. Vous pouvez l’utiliser pour indiquer à votre moteur de recherche de trouver l’un des différents synonymes. OU élargira la portée de votre recherche. Le terme booléen NOT vous permet d’exclure les résultats non liés. Par exemple, si vous recherchez des informations sur les impôts en Amérique, mais que vous continuez à obtenir des résultats pour l’Amérique latine, vous pouvez vous concentrer sur les bons résultats en utilisant l’expression de recherche booléenne « taxes AND America NOT Latin ». Si vous utilisez Google, NOT est représenté par un signe moins.
George Boole, un théoricien de l’algèbre
George Boole est le créateur de la logique moderne, fondée sur une structure algébrique et sémantique que l’on appelle algèbre de Boole en son honneur. De 1844 à 1854, il crée une algèbre binaire, dite booléenne, n’acceptant que deux valeurs numériques : 0 et 1. Cette algèbre, qui présente, entre autre, une affinité avec les états électriques “inactif” et “actif”, aura de nombreuses applications en téléphonie et en informatique. Les travaux précurseurs de Boole, s’ils sont théoriques à la base, n’en trouveront pas moins des applications primordiales. Dès 1867 en effet, le logicien Charles Sanders Peirce (1839-1914) [considéré comme le fondateur du courant pragmatiste avec William James ainsi qu’un des plus grands logiciens], qui était aussi professeur de mathématiques et d’astronomie à l’université d’Harvard, commence à diffuser les idées principales de l’algèbre de Boole aux États-Unis.
George Boole (1815-1864)
Mathématicien et logicien anglais qui a aidé à établir la logique symbolique moderne et une algèbre de la logique, maintenant appelée algèbre booléenne. En remplaçant les opérations logiques par des symboles, Boole a montré que les opérations pouvaient être manipulées pour donner des résultats logiquement cohérents. L’algèbre logique de Boole est essentiellement une algèbre de classes, basée sur des concepts tels que complément et union de classes. L’étude de la logique mathématique ou symbolique s’est développée principalement à partir de ses idées et est à la base de la conception de circuits informatiques numériques. Les algèbres booléennes trouvent également des applications importantes dans des domaines aussi divers que la topologie, la théorie de la mesure, les probabilités et les statistiques. Boole a également écrit d’importants travaux sur les équations différentielles et d’autres branches des mathématiques.
http://images.math.cnrs.fr/+George-Boole-est-mort-il-y-a-cent+.html
https://history-computer.com/george-boole-complete-history/
https://history-computer.com/boolean-logic-complete-guide/
https://stringfixer.com/fr/Boolean_equation