Sophie Germain, une mathématicienne inconnue, la première femme à remporter un prix de l’Académie des sciences de Paris pour son article sur l’élasticité
Une des premières mathématiciennes de l’époque moderne, étudiante clandestine, Sophie Germain n’a pas hésité à s’attaquer à certains des problèmes mathématiques les plus complexes.
Une enfance en bibliothèque
Sophie Germain (1776-1831) est née le 1er avril 1776 à Paris dans un monde en changement. C’était le siècle des Lumières et de l’émergence de la science moderne marquée par l’édition, entre 1751 et 1772, de la Grande Encyclopédie de Diderot à laquelle a participé le mathématicien D’Alembert. C’était aussi le temps des révolutions, avec l’indépendance américaine proclamée le 4 juillet 1776 et l’annonce de l’écroulement de l’Ancien régime en France. Le père de Sophie Germain, négociant en tissus, plus tard député du Tiers État en 1789 puis directeur de la Banque de France, créée par Napoléon en 1800, allait faire partie de cette bourgeoisie qui allait supplanter la noblesse et prendre le pouvoir.
Si on pouvait parler de révolution en sciences et en politique, ce n’était pas le cas dans le domaine des mœurs ! Les sciences étaient une affaire d’homme, les femmes étaient cantonnées, elles, aux seules sciences ménagères ! Dans ces temps troublés, le père de Sophie veilla à ce que sa fille restât à la maison. Sophie Germain passa ainsi sa jeunesse dans la bibliothèque de son père.
Une lecture l’a profondément marquée à l’âge de 13 ans : la vie et la mort d’Archimède. Selon la légende, Archimède traçait des cercles sur le sable lorsqu’un soldat romain lui fit de l’ombre en passant. « Ne dérange pas mes cercles » lui aurait dit Archimède. Le soldat le prit mal et le tua.
Elle se passionna ainsi pour l’œuvre d’Archimède et pour les mathématiques.
Une étudiante clandestine
Sophie aurait aimé étudier les mathématiques à l’École Polytechnique, qui venait d’être créée, mais l’école était interdite aux femmes (les filles ne purent accéder à l’École Polytechnique qu’après 1970 dans la foulée de mai 68, tandis que la première professeure n’y fut nommée qu’en 1992). Elle se procura plutôt les notes de cours et échangea par écrit avec certains des professeurs, dont Lagrange, en prenant le nom d’Antoine Auguste Le Blanc. C’était son seul moyen d’être prise au sérieux car les scientifiques de l’époque ne concevaient pas qu’une femme puisse s’intéresser aux sciences, encore moins y exceller.
Un défi en mathématiques pures : le Théorème de Fermat
Exceller au point de s’attaquer au fameux Théorème de Fermat, sujet par excellence en mathématiques pures.
Vers 1670 le mathématicien Fermat pose une hypothèse fameuse : Il n’existe pas de nombres entiers non nuls x, y et z tels que xª + yª = zª dès que a est un entier strictement supérieur à 2. Cette hypothèse aura fait travailler des générations de mathématiciens avant qu’Andrew Wiles n’en découvre une preuve de près de mille pages en 1994 !
Une difficile reconnaissance par les pairs masculins
En dehors de la théorie des nombres, Sophie Germain, qui s’affichait maintenant sous son propre nom, s’intéressa à un phénomène de vibration découvert en 1807 par le physicien Ernst Chladni : en saupoudrant de sable un disque de cuivre et en le frottant avec un archet, il obtenait d’étonnantes figures géométriques. Pour expliquer ce phénomène, l’Institut de France ouvrit un concours sur la formulation mathématique des surfaces élastiques. Sophie Germain tenta pendant plus de dix ans de résoudre ce problème.
Elle fut la seule à déposer un mémoire à ce sujet, qui fut deux fois refusé à cause d’erreurs. Lagrange, qui était membre du jury, évaluait que les outils mathématiques nécessaires, à savoir le calcul des variations, n’était pas assez développé. Par ailleurs, Sophie Germain s’opposait à un mathématicien réputé de l’époque, Poisson, qui privilégiait (à tort) une approche moléculaire du phénomène. Sophie réussit cependant à proposer une solution en 1816. Le jury lui accorda le prix, une médaille en or, pesant 1 kg selon certains. Mais Sophie ne se présenta pas pour la recevoir : elle estimait que le jury n’avait pas évalué son travail à sa juste valeur, notamment parce qu’elle était une femme. Elle a quand même été la première femme reçue par l’Institut, en dehors des épouses des savants masculins, bien entendu!
Elle poursuivit quand même ses recherches, mais le mémoire qu’elle déposa en 1825 fut tout simplement ignoré par le jury où figurait Poisson!
Les résultats de son travail ont pourtant permis de nombreuses réalisations, dont la tour Eiffel.
Fin de vie
Sophie Germain a aussi travaillé sur l’esprit des sciences et a publié Considérations générales Sur L’État des Sciences et des Lettres qui ont beaucoup inspiré Auguste Comte, père du positivisme et précurseur de la sociologie.
Elle est décédée en 1831, à Paris, d’un cancer du sein, juste avant que, sur la proposition de Carl Friedrich Gauss, l’Université de Göttingen lui accorde un doctorat honorifique.
Sur son certificat de décès, elle est présentée comme « rentière » ce qui, à cette époque, était plus honorable pour une femme que d’être présentée comme « mathématicienne »…
Elle était fille unique d’un riche marchand de soie. Elle se prit de passion pour les mathématiques à l’âge de 13 ans, après avoir lu à la bibliothèque un chapitre sur la vie d’Archimède. Elle se procure les cours de l’École polytechnique, réservée aux hommes, en empruntant l’identité d’un ancien élève, Antoine Auguste Le Blanc. Elle envoie ses remarques à Joseph-Louis Lagrange qui finit par découvrir l’imposture en la convoquant du fait de ses brillantes réponses. Il devient l’ami et le mentor de la jeune fille.
Sophie Germain, la mathématicienne de génie sans qui la tour Eiffel n’existerait pas
Un théorème mathématique porte le nom de Sophie Germain. Sans ses travaux, un projet tel que la tour Eiffel n’aurait pas pu voir le jour.
Lorsque la Tour Eiffel a été érigée, on a inscrit sur cette haute structure les noms de soixante-douze savants. Mais on ne trouve pas dans cette liste le nom de cette femme de génie, dont les recherches ont tant contribué à établir la théorie de l’élasticité des métaux : Sophie Germain. A-t-elle été exclue de cette liste pour la même raison qu’elle était inéligible à l’Académie — parce qu’elle était une femme ? Si tel était le cas, la honte serait grande pour ceux qui ont été responsables d’une telle ingratitude envers celle qui avait si bien servi la science et qui, par ses réalisations, avait gagné une renommée enviable.
Sophie Germain ne fait pas partie des femmes dont les inventions ont été attribuées à des hommes (elles sont nombreuses), mais son nom a cependant été effacé de l’histoire des sciences et de la mémoire collective. La mathématicienne était pourtant une scientifique extraordinaire, aussi inspirante que le furent les génies déjà tant nommés. « Comme le grand géomètre de Syracuse, Archimède, qui a toujours été son inspiration pour l’étude des mathématiques, elle serait morte plutôt que d’abandonner un problème qui engageait toute son attention.
SI une fine feuille de métal circulaire est fermement fixée au centre par une pince, et si un archet de violon est tiré sur son bord, une note de musique sera produite. La plaque est mise en vibration par l’archet ; les vibrations ne montent pas toutes en même temps et ne descendent pas toutes en même temps, mais elles se divisent en un nombre pair de secteurs, disons six ou huit, et lorsqu’un secteur monte, le secteur de chaque côté descend. La ligne entre deux secteurs adjacents ne monte ni ne descend, mais reste au repos. Si le sable est dispersé uniformément sur la plaque avant que la note de musique ne soit produite, il sera secoué par les parties les plus en mouvement et s’accumulera dans les lignes de repos, ou « lignes nodales », comme on les appelle. Les différentes notes de musique provoquent une division différente de la plaque, et l’état de vibration de la plaque est rendu évident à l’œil par les lignes de sable qui y sont tracées. Cette expérience, très frappante, qui est encore réalisée dans tous les laboratoires de physique, a été exposée à Paris, peu après sa découverte par Chladni, en 1808. Elle fit grand bruit, et une commission fut nommée pour la répéter avec diverses modifications, et pour en faire un rapport. L’Institut de France, à la suggestion de Napoléon, offrit son grand prix pour une discussion mathématique du phénomène. Les grands mathématiciens ne manquaient pas à Paris à cette époque – Lagrange, Laplace, Legendre, Poisson, Fourier – mais aucun d’entre eux n’était enclin à entreprendre cette question ; Lagrange, en fait, avait déclaré qu’elle ne pouvait être résolue par aucune des méthodes mathématiques alors connues. L’offre fut renouvelée deux fois par l’Institut, et en 1816 le prix fut décerné à une femme, Mlle Sophie Germain. Il est très remarquable qu’une distinction aussi grande que celle d’avoir reçu le prix de l’Institut de France pour une discussion mathématique approfondie n’aurait pas dû préserver le nom de Sophie Germain de l’oubli, mais ce n’est pas le cas. Il n’y a probablement pas une vingtaine de personnes dans ce pays qui n’aient jamais entendu parler d’elle, et dans son propre pays, elle n’est généralement pas mentionnée parmi les femmes célèbres. Pour prouver que les femmes peuvent être de pures mathématiciennes, Mme Somerville a dû, en dehors de l’Italie et de la Russie, faire cavalier seul. C’est malheureux, car les détracteurs de son sexe ont soutenu que son travail, bien que extrêmement profond, n’était pas remarquable pour l’originalité. Cette accusation ne peut être portée contre Sophie Germain. Elle a fait preuve d’une grande audace en s’attaquant à une question physique qui était à l’époque entièrement hors de portée du traitement mathématique, et dont les cas les plus compliqués ne se sont pas encore soumis à l’analyse. L’équation de la lamine élastique, que l’on appelle encore aujourd’hui l’équation de Germain, a constitué le point de départ d’une nouvelle branche de la théorie de l’élasticité. Dans ses dernières années, Sophie Germain s’est tournée vers les questions de philosophie, et une haute autorité allemande a récemment découvert que ses écrits philosophiques contiennent le germe de la philosophie positive de Comte. Il est curieux qu’une femme si digne de reconnaissance ne l’ait pas reçue à un plus haut degré ; il faut y voir un de ces accidents par lesquels la distribution des louanges au mérite est trop souvent mal réglée. Un mathématicien, dont le sujet est si éloigné des préoccupations ordinaires des hommes, doit être un très grand mathématicien pour que le grand public en entende parler. Sophie Germain, en plus de mériter d’être rappelée pour ses contributions à la science, avait une personnalité charmante, et les quelques détails qui ont été conservés sur sa vie ne seront pas sans intérêt. Ils s’appuient sur un article de Libri, le mathématicien italien, paru dans le « Journal des Débats » au moment de sa mort. Des auteurs ultérieurs, dont l’auteur de la biographie préfixée à la nouvelle édition de ses œuvres philosophiques, parue en 1879 (Paris : P. Ritti), n’ont guère ajouté d’éléments importants à son récit.
Le 1er avril 1776, dans une modeste maison de la rue Saint Denis, à Paris, naît Marie Sophie Germain. Ses parents sont Ambroise François Germain et Marie Madeleine Gruguelu. On ne sait pas grand-chose de sa famille. On sait seulement que son père, habile orfèvre, appartenait à la bourgeoisie cultivée et libérale, et qu’il était le partisan, sinon l’ami, des philosophes et des économistes politiques. Il est évident qu’elle a dû passer ses premières années dans une famille où les sujets de conversation sérieux ne manquaient pas. Elle a rapidement fait preuve d’une grande maturité intellectuelle et d’une remarquable profondeur de sentiments. Ses sombres anticipations concernant l’avenir de son pays étaient pour elle une cause distincte de souffrance, et elle cherchait une occupation suffisamment absorbante pour détourner son attention de ses craintes. À l’âge de treize ans, elle parcourait un jour les pages de l' »Histoire des mathématiques » de Montluca dans la bibliothèque de son père, lorsqu’elle tomba sur le récit éloquent de la mort d’Archimède – comment il était si absorbé dans l’examen d’une figure géométrique qu’il n’entendit rien de la prise de Syracuse, ni du pillage de la ville, et que, lorsqu’un soldat romain apparut devant lui, il mourut de ses mains sans lever les yeux de son travail. Elle conçut une passion soudaine pour une science qui pouvait procurer une concentration aussi absolue et un oubli aussi total des soucis et des chagrins de la vie, et elle résolut à ce moment de se consacrer à l’étude des mathématiques. Cette résolution, elle la mit à exécution. Elle n’avait pas de professeurs, elle avait peu de livres, mais elle avait une réserve illimitée d’énergie. Elle étudiait jour et nuit. Sa famille, alarmée par tant d’ardeur, s’efforça de détourner son attention vers des activités plus féminines. Ils ont essayé d’éteindre son feu et de lui enlever ses vêtements la nuit, mais on l’a retrouvée le matin enveloppée dans des couvertures, absorbée dans ses études dans une pièce si froide que l’encre était gelée dans l’encrier. C’est une curieuse coïncidence que Mme Somerville, à la même époque, dans son petit village d’Écosse, était obligée de s’envelopper dans des couvertures pour poursuivre ses études avant le petit déjeuner, car toute sa journée devait être consacrée à la pratique de la musique et de la peinture, et à ses leçons chez le pâtissier.1 Devant une force de volonté si remarquable à son âge, la famille de Sophie Germain finit par céder, et on la laissa disposer de son temps et de ses talents à sa guise./Sophie-Germain-78997156b-56aa221d3df78cf772ac852e.png)
Mais quelle que soit l’énergie déployée, les mathématiques supérieures représentent un long et pénible parcours d’étude pour celui qui veut les maîtriser. Sophie Germain a poursuivi ce travail laborieux avec une satisfaction toujours croissante. Vers la fin de sa vie, elle parlait encore avec animation du bonheur qu’elle avait éprouvé lorsqu’elle s’était trouvée en mesure de reprendre le calcul différentiel de Cousin. Mais bientôt une nouvelle difficulté se présenta. Il était absolument nécessaire pour son progrès qu’elle lise certains ouvrages écrits en latin, et elle ne comprenait pas cette langue. Seule et sans aide, elle entreprend de l’apprendre et, en peu de temps, elle est capable de lire les œuvres d’Euler et de Newton. Son ambition s’élargit alors, et, entraînée par l’esprit philosophique qui régnait dans la grande encyclopédie, elle étendit ses lectures à tout le domaine des sciences, et jeta les bases de cet ouvrage qui, quarante ans plus tard, devait lui assurer une place parmi les fondateurs de la philosophie positive.
En 1794, l’École Polytechnique est fondée. Lagrange, Prony, Fourcroy, Monge, sont parmi ses professeurs. Sophie Germain est alors âgée de dix-huit ans. Soucieuse de profiter d’un moyen d’instruction aussi précieux, elle se procura des cahiers d’élèves, notamment des cours de chimie de Fourcroy, et d’analyse de Lagrange. Elle fit plus encore. Les étudiants avaient l’habitude de remettre aux professeurs, à la fin d’un cours, leurs observations écrites sur les conférences auxquelles ils avaient assisté. Sous le nom supposé d’un étudiant, Le Blanc, elle envoya ses cahiers à Lagrange. Celui-ci les remarqua, les loua publiquement, découvrit leur véritable auteur, et, ayant fait sa connaissance, devint l’ami et le conseiller du jeune mathématicien. Les circonstances dans lesquelles elle fut découverte, l’approbation de l’illustre auteur de la « Mécanique Analytique », sa jeunesse, quelques détails sur ses études, tout cela excita l’attention, et lui procura des amis sympathiques. Bientôt elle avait établi des relations, soit directement, soit par correspondance, avec tous les savants de l’époque. Chacun sollicitait l’honneur d’être présenté à elle, des ouvrages savants lui étaient dédiés, et sa maison devint un centre pour la brillante conversation des hommes les plus distingués de l’époque.
Quelques années plus tard, le grand ouvrage de Gauss sur la « Théorie des nombres » parut. Mlle Germain s’intéresse aussitôt à ce sujet. Elle y fit de nombreuses recherches et, sous le pseudonyme de Le Blanc, elle envoya ses notes au célèbre professeur de Göttingen, persuadée, écrit-elle, qu' »il ne dédaignera pas d’éclairer de ses conseils un amateur enthousiaste de cette science qu’il cultive avec un si brillant succès. » M. Le Blanc était loin d’être un simple amateur, et Gauss s’en est vite rendu compte. Sa réponse contenait une reconnaissance chaleureuse de ses talents, et une relation amicale s’est maintenue entre eux pendant plusieurs années sans qu’il ne se rende compte du sexe de sa correspondante.
En 1808, Sophie Germain concourut au prix offert par l’Institut pour le meilleur mémoire exposant la théorie mathématique des surfaces élastiques, et la confrontant à l’expérience. Elle avait déduit l’équation de ces surfaces d’une certaine hypothèse concernant les forces d’élasticité, mais il y avait une erreur dans ses mathématiques, et son équation n’était pas correcte. Lagrange, à qui l’article avait été adressé, déduisit de la même hypothèse l’équation qui est toujours reconnue comme correcte. Elle n’a pas reçu le prix. Deux ans plus tard, elle envoya un second mémoire, dans lequel la même équation est donnée correctement, et une hypothèse plus compliquée conduit à l’équation de l’état de choses qui s’obtient aux limites de la plaque élastique. Elle avait également confirmé sa solution théorique par une longue série d’expériences. Cet article a reçu une mention honorable. Nullement découragée, elle tente une troisième fois sa chance et reçoit le prix, bien que la commission ne soit pas absolument satisfaite de la rigueur de sa démonstration. L’équation de Germain pour les plaques élastiques est toujours l’équation fondamentale de la théorie. Ses équations limites n’ont pas résisté à l’épreuve du temps ; Poisson, quatorze ans plus tard, a donné un ensemble différent d’équations limites basées sur une hypothèse différente, et Kirchoff, en 1850, a montré qu’aucune des deux hypothèses n’était tenable, et qu’aucun des ensembles d’équations n’était correct.
En 1824, elle envoya à l’Institut un autre article intitulé « On the Employment of the Thickness in the Theory of Elastic Surfaces ». Ce document a été confié à une commission composée de Poisson, Prony et Laplace, afin qu’elle fasse un rapport. Ils n’ont jamais remis leur rapport, et elle n’a jamais pu reprendre possession du manuscrit. Il y a quelques années seulement, on le découvrit parmi les papiers de Prony, et il fut réimprimé en entier, dans un supplément au « Journal des Mathématiques » de Liouville.
N’étant pas gâtée par son succès, Sophie Germain poursuivit ses études avec tout son enthousiasme d’antan. Elle assiste aux séances de l’Académie des Sciences, se tient au courant des recherches scientifiques de ses contemporains, et trouve le temps de rendre divers services amicaux à ses connaissances. Elle a contribué aux « Annales de Physique et de Chimie » à un examen des principes qui conduisent aux lois du mouvement des solides élastiques. Dans cet article, elle établit, en opposition à Poisson, qu’aucune hypothèse concernant la constitution moléculaire des corps n’est nécessaire dans une discussion sur l’élasticité. Ses vues sur ce sujet ont été abondamment confirmées. Deux de ses articles dans le « Journal de Crelle » – l’un sur la courbure des surfaces, et l’autre sur la théorie des nombres – ont été composés par elle pendant le bruit du canon de juillet 1830. Son espoir de trouver une absorption profonde dans l’étude des mathématiques n’avait pas été déçu.
De nombreux témoignages attestent le charme de son caractère et de sa conversation. Elle était imprégnée d’un amour pur de la science, et elle était remarquablement indifférente à sa propre renommée. Elle se réjouissait lorsque des idées qu’elle avait laissé échapper dans la conversation étaient appropriées par d’autres. Peu importe, disait-elle, de qui vient une idée ; il importe seulement qu’elle soit vraie et utile. Elle définissait la renommée comme le petit espace que l’on occupe dans le cerveau de ses voisins – une définition que Schopenhauer a reprise depuis. Elle considérait la vertu comme un sens de l’ordre, que l’intelligence cultivée doit admirer, même si le cœur ne l’aime pas. Sa conversation était pleine de gaieté et de fraîcheur, et portait des marques constantes d’originalité de pensée, et d’un traitement poétique de ses pensées. Elle est morte à l’âge de cinquante-cinq ans. Sa tombe au Père la Chaise, à quinze pas de celle du Comte, est dans un état négligé. La balustrade est rouillée, la pierre est tombée, la bordure de buis est sauvage et envahie par la végétation.
Les écrits philosophiques de Sophie Germain ont été donnés au monde deux ans après sa mort, par son neveu, Lherbette. Outre quelques pensées détachées, ils consistent en un long article intitulé « Considérations sur l’état des sciences et des lettres aux différentes époques de leur culture. » Son idée principale est l’extension des principes de droit, et de l’interaction harmonieuse des causes qui prévalent dans les sciences physiques, aux régions de la politique, de la morale et de l’art – la même idée que Comte a exposée avec beaucoup plus de détails dans son « Cours de Philosophic Positive. » La dette de Comte envers Condorcet et Saint-Simon a souvent été mentionnée. Ce n’est que récemment que l’on a découvert à quel point Sophie Germain l’avait devancé dans les traits principaux de son système. Dühring, dans son « Histoire critique de la philosophie depuis ses débuts jusqu’à nos jours » (troisième édition, Leipsic, 1878), dit, après avoir donné un résumé complet de son œuvre : « On voit par ce qui précède que le positivisme que l’on trouve, sans l’emploi du mot, dans les écrits de Sophie Germain, contient les traits essentiels de celui qui a été jusqu’ici associé au nom d’Auguste Comte. » Le « Zeitschrift für Philosophic » a publié deux longs articles de Göring intitulés : « Sophie Germain comme prédécesseur de Comte. » Ses « Considérations » sont encore très intéressantes à lire et mériteraient d’être traduites.
1 La loi générale selon laquelle l’apprentissage des femmes doit être obtenu par des mesures héroïques, si tant est que ce soit le cas, n’est pas encore dépassée. Ellen Watson, la jeune femme très douée, élève de Clifford, qui mourut au Cap de Bonne-Espérance à un jeune âge, étudiait avant le petit déjeuner, car elle devait passer la journée à enseigner à ses jeunes frères et sœurs ; et le tout dernier numéro du « Nineteenth Century » contient le récit d’une jeune fille dont la famille compatissante lui garantit deux heures ininterrompues chaque jour pour une sieste dans l’après-midi en raison de sa santé délicate, sans savoir que sa somnolence de l’après-midi est due à des heures de dur labeur avant le petit déjeuner – travail pour lequel, il va sans dire, elle n’oserait pas demander deux heures ininterrompues l’après-midi.
Mathématicienne française connue pour ses travaux en théorie des nombres et ses contributions aux mathématiques appliquées de l’acoustique et de l’élasticité. Germain s’est formée en autodidacte à partir de livres et de notes de cours fournies par des amis masculins de l’École polytechnique, à laquelle elle n’était pas autorisée à assister en tant que femme. Utilisant un pseudonyme masculin, M. LeBlanc, elle correspond avec Lagrange qui reconnaît ses compétences et parraine ses travaux. Elle a réalisé une preuve limitée du dernier théorème de Fermat, pour tout nombre premier inférieur à 100 lorsque certaines conditions sont remplies. En 1816, elle a remporté un prix parrainé par Napoléon pour une explication mathématique des figures de Chladni, la vibration des plaques élastiques. Elle est morte à l’âge de 55 ans, d’un cancer du sein.
L’une des pionnières de la théorie de l’élasticité, Germain a remporté le grand prix de l’Académie des sciences de Paris pour son essai sur le sujet intitulé « Recherches sur la théorie des surfaces élastiques ».
Son travail sur le dernier théorème de Fermat a fourni une base aux mathématiciens explorant le sujet pendant des centaines d’années.
Événements historiques
1816-01-08 Sophie Germain est la première femme à remporter un prix de l’Académie des sciences de Paris pour son article sur l’élasticité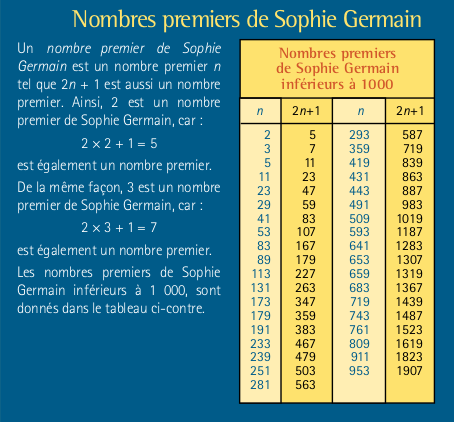
https://femmessavantes.pressbooks.com/chapter/sophie-germain-mathematicienne-1776-1831/
https://todayinsci.com/G/Germain_Sophie/GermainSophieBio.htm
https://www.onthisday.com/people/sophie-germain