Gödel a commencé à en parler lors de son véritable examen, disant au juge que les États-Unis pourraient devenir une dictature – « Je peux le prouver ! » – avant que ses amis (dont Albert Einstein) ne parviennent à le faire taire pour que le processus de naturalisation puisse se dérouler comme prévu. C’est le genre d’éruption indisciplinée que Stephen Budiansky présente avec un effet puissant et divertissant dans « Journey to the Edge of Reason », son récit de la vie et de l’œuvre de Gödel. Le « théorème d’incomplétude » de Gödel, qu’il a présenté en 1930, alors qu’il avait 24 ans, a renversé l’hypothèse de sa profession selon laquelle les mathématiques devraient être capables de prouver qu’un énoncé mathématique est vrai. La preuve de Gödel a abouti à un énoncé mathématique qui était vrai mais indémontrable.
Pour les lecteurs intéressés, Budiansky fournit une annexe qui parcourt la preuve de Gödel, étape par étape, mais une connaissance granulaire de la logique formelle n’est pas essentielle pour que quiconque puisse profiter de cette biographie émouvante. Budiansky – dont la production impressionnante et variée comprend un roman, un livre sur Oliver Wendell Holmes, un autre sur la violence de l’après-guerre civile et une histoire de chats – porte l’intérêt d’un polymathe sur un homme dont la vie a croisé les bouleversements politiques et philosophiques du 20ème siècle. Gödel est né en 1906 dans une famille germanophone prospère à Brünn, dans la partie morave de l’empire des Habsbourg. Son enfance fut heureuse, dans ce que l’écrivain Stefan Zweig appelait «l’âge d’or de la sécurité», avant l’effondrement de l’empire avec la Première Guerre mondiale. Dès l’âge de 4 ans, Gödel était connu sous le nom de «Herr Warum» ou «M. Pourquoi. » Il dira plus tard à un psychiatre qu’il était « toujours curieux, questionnant l’autorité, exigeant des raisons ». Il a vécu cela comme un délice, pas un fardeau : « Le but le plus élevé de ma vie (conçu à la puberté) est le plaisir de la cognition. »
Budiansky raconte dans son intégralité la maturité intellectuelle de Gödel – son déménagement à Vienne en 1924, où il étudia les mathématiques après avoir décidé que la physique était « logiquement si désordonnée » ; sa participation au célèbre Cercle de Vienne, qui s’est chargé de discuter des transformations de la pensée scientifique occasionnées par des idées révolutionnaires comme la théorie de la relativité d’Einstein.
Vienne à l’époque était intellectuellement exaltante et politiquement périlleuse, un lieu d’érudition et d’enseignement supérieur étonnant qui fonctionnait également comme «la capitale mondiale des excentriques, des paranoïaques, des mégalomanes et des théoriciens du complot», écrit Budiansky. Fait intéressant et aussi tragique, Gödel lui-même en viendrait à incarner ce fouillis insoutenable, oscillant entre des accès de lucidité exigeante et d’illusion totale. Non seulement Budiansky propose une discussion claire du théorème d’incomplétude avec les éloges qu’il a suscités ; il prend soin d’ancrer la preuve dans la vie, évitant le genre d’interprétations sombres qui ont si souvent fait que Gödel se sentait incompris. Gödel avait réduit en miettes la compréhension établie des mathématiques – ou l’avait-il fait ? Gödel a refusé la conclusion nihiliste tirée par certains de son travail : que parce qu’il y avait des vérités qui n’étaient pas prouvables, rien de mathématique n’était vraiment connaissable. Il a plutôt tiré des conclusions optimistes, choisissant de souligner qu’il y aurait toujours de nouvelles vérités mathématiques à découvrir. Si quoi que ce soit, écrit Budiansky, Gödel croyait que son résultat « signifiait que l’ingéniosité humaine serait nécessaire pour construire de nouvelles voies vers les vérités qui étaient là-bas, attendant d’être découvertes ».
C’est cet accent mis sur les implications humaines et humaines de la vie et de l’œuvre de Gödel qui donne à ce livre son attrait fascinant. Budiansky consacre un chapitre à la décision de son sujet de quitter l’Autriche occupée par les nazis – une « année de vie indécise », écrit Budiansky, alors que les finances de la famille étaient au plus bas. Gödel n’était pas juif et a même voté en faveur de l’incorporation de l’Autriche dans le Reich ; mais en tant que mathématicien révolutionnaire avec de nombreux amis juifs, il aurait sans aucun doute été soupçonné d’un régime gouverné par des théories cinglées sur un « indice de valeur raciale » et une « cosmogonie glaciaire » remplie de « glace cosmique ». Gödel a trouvé une maison à l’Institute for Advanced Study du New Jersey, où les chercheurs étaient bien payés pour poursuivre leurs intérêts de recherche sans la responsabilité d’une charge d’enseignement – une configuration si pépère que les professeurs jaloux de Princeton l’appelaient « l’Institut » pour les salaires avancés.
Gödel pouvait faire de longues promenades avec son collègue érudit de l’institut Einstein, qui a parrainé la demande de citoyenneté de Gödel et l’a appelé le plus grand logicien depuis Aristote, mais il était ravagé par des maux physiques et des conditions nerveuses. Un médecin lui a dit qu’il avait un ulcère qui saignait, ce qu’il a étrangement refusé de croire, même s’il était aussi un hypocondriaque qui se soignait lui-même. Il a souscrit à toutes sortes de théories du complot, insistant sur le fait que « rien n’arrive sans raison » et que la raison était presque toujours cachée. La liberté illimitée qu’il avait à l’institut s’est avérée à double tranchant, observe Budiansky. Dans un sens, cela a sauvé la vie de Gödel ; mais cela a également permis à sa conscience de se promener dans les endroits les plus sombres, sans les contrôles sur ses angoisses expansives que les interactions avec le monde ordinaire auraient pu autrement fournir. « Journey to the Edge of Reason » fait un usage abondant et éclairant de la correspondance et des journaux de Gödel, y compris un journal, tenu dans une sténographie spéciale, qui n’avait jamais été traduit auparavant. Budiansky est judicieux dans ses interprétations, préférant surtout laisser ses thèmes émerger de l’histoire captivante qu’il raconte. Gödel est décédé en 1978, après des semaines de famine à un poids de 65 livres. Son psychiatre avait enregistré la descente en spirale de Gödel dans le dégoût de soi et la paranoïa. Mais un « pourquoi » satisfaisant pour la fin ultime de Herr Warum reste insaisissable. Le médecin traitant a écrit que la cause du décès était « plus d’apathie et de résignation qu’un effort suicidaire volontaire actif ».
Le mathématicien qui insistait joyeusement sur le fait que sa preuve ouvrait un espace à la créativité humaine avait succombé aux visions vouées à l’échec de son propre désespoir. C’est une incohérence apparente que Gödel aurait pu remarquer si elle lui avait été présentée dans les termes froids de la logique formelle, mais comme cette biographie vibrante l’élucide si magnifiquement, la vérité d’une vie ne peut jamais être prouvée ; il ne peut qu’être montré.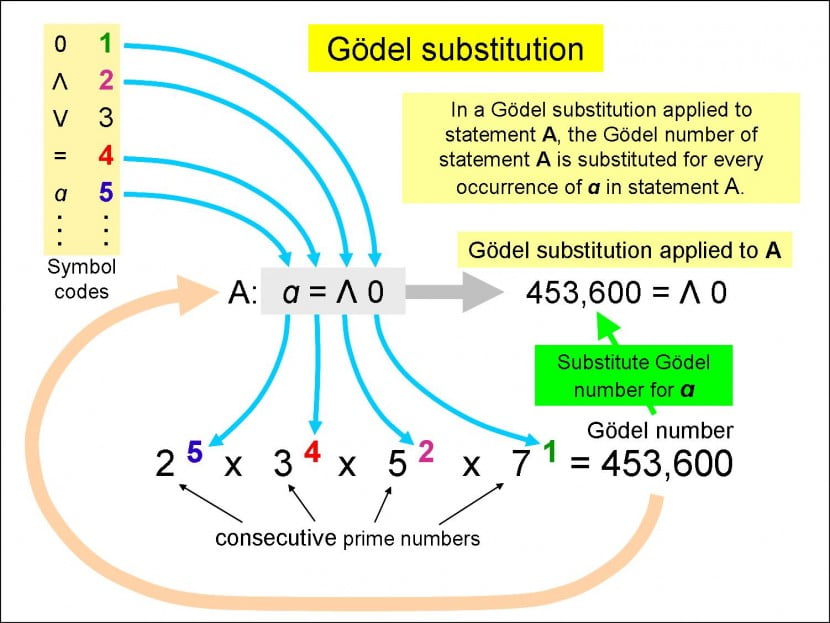
Kurt Godel, un grand mathématicien
Kurt Gödel était un éminent mathématicien autrichien du XXe siècle. Il était également philosophe et logicien. Après Gottlob Frege et Aristote, il fut l’un des plus grands logiciens de l’histoire. Il a influencé l’école de pensée scientifique et philosophique du XXe siècle. En 1931, il publie ses théorèmes d’incomplétude. Il a développé une technique qui s’appelle maintenant la numérotation de Gödel. Il avait prouvé que l’hypothèse du continuum et l’axiome du choix pouvaient être réfutés. En outre, il a considérablement contribué au développement de la théorie de la preuve.
Kurt Friedrich Gödel est né le 28 avril 1906 à Brünn, en Autriche-Hongrie, dans une famille d’origine allemande. Son père, Rudolf Gödel, était catholique et directeur dans une usine textile. Il avait des liens étroits avec sa mère protestante et est resté dans une correspondance constante avec elle. Il y a une longue liste de citoyennetés que Gödel a prises. À l’âge de 12 ans, il a reçu la nationalité tchécoslovaque lors de l’éclatement de l’empire austro-hongrois. Il s’est toujours senti excommunié en tchécoslovaque, alors quand il est devenu adulte, il a choisi la nationalité autrichienne. Par la suite, l’Allemagne a annexé l’Autriche et, par conséquent, les citoyens autrichiens sont devenus allemands, tout comme Gödel en 1938. Après la Seconde Guerre mondiale, il a déménagé en Amérique où il a demandé la citoyenneté américaine. Gödel a été surnommé par sa famille comme ‘M. Pourquoi ? Pour sa curiosité toujours insatiable de connaître l’inconnu. Dans son enfance, il a souffert de fièvre rhumatismale et d’épisodes de mauvaise santé pour le reste de sa vie. Il a reçu sa première éducation dans une école luthérienne de Brünn. Il est ensuite allé au Deutsches Staats-Realgymnasium avec une spécialisation en études religieuses, langues et mathématiques. Au départ, il s’intéressait aux langues et s’est ensuite pris aux mathématiques dans les années 1920. Dans son adolescence, il étudie les critiques d’Isaac Newton, l’œuvre d’Emmanuel Kant et la théorie des couleurs de Goethe.
Suivant les traces de son frère, Gödel a rejoint l’Université de Vienne. La physique théorique était son choix initial d’étudier en tant que majeure, mais plus tard, il a montré une inclination pour la philosophie et les mathématiques. En lisant Metaphysische Anfangsgründe der Naturwissenschaft de Kant, Gödel a essayé d’adopter le concept de réalisme mathématique. Il a participé au Cercle de Vienne avec Hans Hahn et Moritz Schlick. Son intérêt pour la logique mathématique a été stimulé par l’introduction de Russell à la philosophie mathématique qui a été discutée dans un séminaire par Moritz. Godel croyait que la logique mathématique est le fondement de toutes les disciplines scientifiques, comprenant toutes les idées et principes pour soutenir la science. Tous ces séminaires et livres ont peut-être piqué l’intérêt de Gödel, mais ce qui l’a vraiment inspiré à consacrer toute sa vie aux mathématiques, c’est une conférence donnée par David Hilbert à Bologne. Il a terminé ses études de doctorat en 1930, qui étaient basées sur la question de savoir si les axiomes sont suffisants pour dériver chaque énoncé dans un système formel.
L’Académie des sciences de Vienne a publié sa thèse et d’autres recherches importantes. Gödel a fait publier ses théorèmes d’incomplétude en 1931. Il est devenu un Privatdozent, maintenant appelé stagiaire, en 1933. La même année, il s’est rendu pour la première fois aux États-Unis après la prise de contrôle d’Adolf Hitler et l’assassinat d’un de ses anciens élèves. Il a rencontré le génie Albert Einstein en Amérique et s’est lié d’amitié. De plus, pendant son séjour en Amérique, il a développé les idées de calculabilité et de fonctions récursives. Il a même prononcé une conférence sur le sujet. À Princeton, l’Institute for Advanced Study l’a invité à diriger une série de conférences en 1934 et elles ont ensuite été publiées. Kurt Gödel a épousé une danseuse divorcée, une femme plus âgée, Adele Nimbursky, après beaucoup d’opposition de la part de ses parents.
Comment fonctionne la preuve de Gödel
En 1931, le logicien autrichien Kurt Gödel a sans doute réalisé l’une des réalisations intellectuelles les plus étonnantes de l’histoire. Les mathématiciens de l’époque recherchaient une base solide pour les mathématiques : un ensemble de faits mathématiques de base, ou axiomes, à la fois cohérents – ne conduisant jamais à des contradictions – et complets, servant de blocs de construction à toutes les vérités mathématiques. Mais les choquants théorèmes d’incomplétude de Gödel, publiés alors qu’il n’avait que 25 ans, ont anéanti ce rêve. Il a prouvé que tout ensemble d’axiomes que vous pourriez poser comme fondement possible des mathématiques sera inévitablement incomplet ; il y aura toujours des faits vrais sur les nombres qui ne peuvent pas être prouvés par ces axiomes. Il a également montré qu’aucun ensemble candidat d’axiomes ne peut jamais prouver sa propre cohérence.
Ses théorèmes d’incomplétude signifiaient qu’il ne pouvait y avoir aucune théorie mathématique de tout, aucune unification de ce qui est prouvable et de ce qui est vrai. Ce que les mathématiciens peuvent prouver dépend de leurs hypothèses de départ, et non d’une vérité de base fondamentale à partir de laquelle toutes les réponses découlent. Au cours des 89 années qui se sont écoulées depuis la découverte de Gödel, les mathématiciens sont tombés sur le genre de questions sans réponse que prédisaient ses théorèmes. Par exemple, Gödel lui-même a aidé à établir que l’hypothèse du continuum, qui concerne les tailles de l’infini, est indécidable, tout comme le problème de l’arrêt, qui demande si un programme informatique alimenté par une entrée aléatoire fonctionnera indéfiniment ou finira par s’arrêter. Des questions indécidables ont même surgi en physique, suggérant que l’incomplétude gôdelienne afflige non seulement les mathématiques, mais – d’une manière mal comprise- la réalité. Voici un aperçu simplifié et informel de la façon dont Gödel a prouvé ses théorèmes.
Numérotation Gödel
La principale manœuvre de Gödel consistait à mapper des déclarations sur un système d’axiomes sur des déclarations à l’intérieur du système – c’est-à-dire sur des déclarations sur des nombres. Cette cartographie permet à un système d’axiomes de parler de lui-même de manière convaincante. La première étape de ce processus consiste à mapper tout énoncé mathématique possible, ou série d’énoncés, sur un nombre unique appelé nombre de Gödel. La version légèrement modifiée du schéma de Gödel présentée par Ernest Nagel et James Newman dans leur livre de 1958, Gödel’s Proof, commence par 12 symboles élémentaires qui servent de vocabulaire pour exprimer un ensemble d’axiomes de base. Par exemple, l’affirmation que quelque chose existe peut être exprimée par le symbole ∃, tandis que l’addition est exprimée par +. Il est important de noter que le symbole s, désignant « successeur de », donne un moyen de spécifier les nombres ; ss 0, par exemple, fait référence à 2. Ces douze symboles se voient alors attribuer les numéros de Gödel de 1 à 12.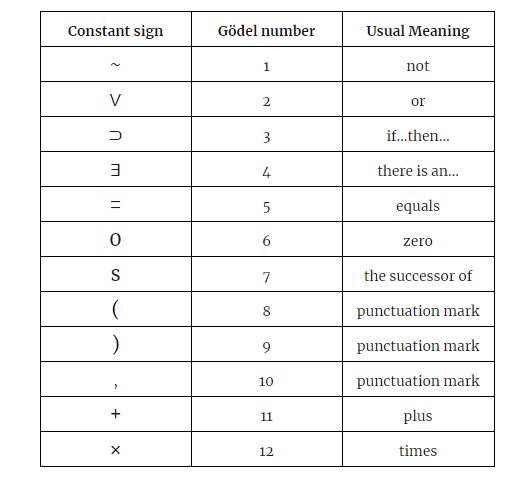
Ensuite, les lettres représentant des variables, commençant par x, y et z, correspondent à des nombres premiers supérieurs à 12 (c’est-à-dire 13, 17, 19, …). Ensuite, toute combinaison de ces symboles et variables – c’est-à-dire toute formule arithmétique ou séquence de formules qui peut être construite – obtient son propre nombre de Gödel. Par exemple, considérons 0 = 0. Les trois symboles de la formule correspondent aux nombres de Gödel 6, 5 et 6. Gödel doit changer cette séquence de trois chiffres en un seul numéro unique – un nombre qu’aucune autre séquence de symboles ne générera. Pour ce faire, il prend les trois premiers nombres premiers (2, 3 et 5), élève chacun au nombre de Gödel du symbole à la même position dans la séquence, et les multiplie ensemble. Ainsi 0 = 0 devient 2 6 × 3 5 × 5 6, soit 243 000 000. Le mappage fonctionne car deux formules ne se retrouveront jamais avec le même nombre de Gödel. Les nombres de Gödel sont des nombres entiers, et les nombres entiers ne se divisent en nombres premiers que d’une seule manière. Ainsi, la seule factorisation première de 243 000 000 est 2 6 × 3 5 × 5 6, ce qui signifie qu’il n’y a qu’une seule façon possible de décoder le nombre de Gödel : la formule 0 = 0.
Gödel est alors allé plus loin. Une preuve mathématique consiste en une séquence de formules. Ainsi, Gödel a également attribué à chaque séquence de formules un numéro de Gödel unique. Dans ce cas, il commence par la liste des nombres premiers comme précédemment — 2, 3, 5 et ainsi de suite. Il élève ensuite chaque nombre premier au nombre de Gödel de la formule à la même position dans la séquence (2 243 000 000 × …, si 0 = 0 vient en premier, par exemple) et multiplie le tout ensemble…..
Théorèmes d’incomplétude de Gödel
Les deux théorèmes d’incomplétude de Gödel sont parmi les résultats les plus importants de la logique moderne et ont des implications profondes pour divers problèmes. Elles concernent les limites de prouvabilité dans les théories axiomatiques formelles. Le premier théorème d’incomplétude stipule que dans tout système formel cohérent \(F\) dans lequel une certaine quantité d’arithmétique peut être effectuée, il existe des énoncés du langage de \(F\) qui ne peuvent être ni prouvés ni réfutés dans \( F\). Selon le deuxième théorème d’incomplétude, un tel système formel ne peut pas prouver que le système lui-même est cohérent (en supposant qu’il est effectivement cohérent). Ces résultats ont eu un grand impact sur la philosophie des mathématiques et de la logique. Il y a eu des tentatives d’appliquer les résultats également dans d’autres domaines de la philosophie tels que la philosophie de l’esprit, mais ces tentatives d’application sont plus controversées. La présente entrée passe en revue les deux théorèmes d’incomplétude et divers problèmes qui les entourent. (Voir aussi l’entrée surFdans lequel une certaine quantité d’arithmétique peut être effectuée, il y a des déclarations de la langue de F qui ne peut être ni prouvé ni réfuté dans F. Selon le deuxième théorème d’incomplétude, un tel système formel ne peut pas prouver que le système lui-même est cohérent (en supposant qu’il est effectivement cohérent). Ces résultats ont eu un grand impact sur la philosophie des mathématiques et de la logique. Il y a eu des tentatives d’appliquer les résultats également dans d’autres domaines de la philosophie tels que la philosophie de l’esprit, mais ces tentatives d’application sont plus controversées. La présente entrée passe en revue les deux théorèmes d’incomplétude et divers problèmes qui les entourent. (Voir aussi l’entrée sur Kurt Gödel pour une discussion des théorèmes d’incomplétude qui les contextualise dans une discussion plus large de son travail mathématique et philosophique.)
Qu’est-ce que le théorème de Gödel ?
Melvin Henriksen, professeur émérite de mathématiques au Harvey Mudd College, propose cette explication :
Donner un énoncé mathématiquement précis du théorème d’incomplétude de Godel ne ferait qu’obscurcir son important contenu intuitif à presque quiconque n’est pas un spécialiste de la logique mathématique. Donc, à la place, je vais le reformuler et le simplifier dans le langage des ordinateurs. Imaginez que nous ayons accès à un ordinateur très puissant appelé Oracle. Comme le font les ordinateurs que nous connaissons, Oracle demande à l’utilisateur de « saisir » des instructions qui suivent des règles précises et il fournit la « sortie » ou la réponse d’une manière qui suit également ces règles. La même entrée produira toujours la même sortie. L’entrée et la sortie sont écrites sous forme d’entiers (ou de nombres entiers) et Oracle n’effectue que les opérations habituelles d’addition, de soustraction, de multiplication et de division (lorsque cela est possible). Contrairement aux ordinateurs ordinaires, il n’y a aucune préoccupation concernant l’efficacité ou le temps. Oracle exécutera les instructions correctement données, peu importe le temps que cela prendra et il ne s’arrêtera que lorsqu’elles seront exécutées, même si cela prend plus d’un million d’années.
Prenons un exemple simple. Rappelez-vous qu’un entier positif (appelons-le N) supérieur à 1 est appelé un nombre premier s’il n’est divisible par aucun entier positif en plus de 1 et N. Comment demanderiez-vous à Oracle de décider si N est premier ? Dites-lui de diviser N par chaque nombre entier entre 1 et N-1 et de s’arrêter lorsque la division sort uniformément ou qu’elle atteint N-1. (En fait, vous pouvez vous arrêter s’il atteint la racine carrée de N. S’il n’y a pas eu de divisions paires de N à ce point, alors N est premier.) Ce que dit le théorème de Godel, c’est qu’il y a des questions correctement posées impliquant uniquement l’arithmétique des nombres entiers auxquelles Oracle ne peut pas répondre. En d’autres termes, il existe des déclarations qu’Oracle ne peut pas évaluer, bien qu’elles soient saisies correctement, pour décider si elles sont vraies ou fausses. De telles assertions sont dites indécidables, et sont très compliquées. Et si vous en apportiez une au Dr Godel, il vous expliquerait que de telles affirmations existeront toujours.
Même si on vous donnait un modèle « amélioré » d’Oracle, appelez-le OracleT, dans lequel une déclaration indécidable particulière, UD, est décrétée vraie, une autre déclaration indécidable serait générée pour prendre sa place. Plus déroutant encore, vous pourriez également recevoir un autre modèle « amélioré » d’Oracle, appelez-le OracleF, dans lequel UD serait décrété faux. Quoi qu’il en soit, ce modèle générerait également d’autres déclarations indécidables et pourrait donner des résultats différents de ceux d’OracleT, mais tout aussi valables. Trouvez-vous cela choquant et proche du paradoxe ? Ce fut encore plus choquant pour le monde mathématique en 1931, lorsque Godel dévoila son théorème d’incomplétude. Godel n’a pas formulé son résultat dans le langage des ordinateurs. Il travaillait dans un système logique défini et les mathématiciens espéraient que son résultat dépendait des particularités de ce système. Mais au cours de la décennie suivante, un certain nombre de mathématiciens – dont Stephen C. Kleene, Emil Post, JB Rosser et Alan Turing – ont montré que ce n’était pas le cas.
Les recherches sur les conséquences de ce grand théorème se poursuivent à ce jour. Toute personne ayant accès à Internet et utilisant un moteur de recherche comme Alta Vista peut trouver plusieurs centaines d’articles de qualité très variable sur le théorème de Godel. Parmi les meilleures choses à lire, cependant, il y a Godel’s Proof d’Ernest Nagel et James R. Newman, publié en 1958 et publié en livre de poche par New York University Press en 1983.
Kurt Gödel (1906-1978)
Mathématicien, logicien et auteur américain d’origine autrichienne de la preuve de Gödel. Il est surtout connu pour sa preuve des théorèmes d’incomplétude de Gödel (1931). Il a prouvé des résultats fondamentaux sur les systèmes axiomatiques montrant dans tout système mathématique axiomatique qu’il existe des propositions qui ne peuvent être prouvées ou réfutées dans les axiomes du système. En particulier, la cohérence des axiomes ne peut être prouvée. Cela a mis fin à cent ans de tentatives d’établir des axiomes pour mettre l’ensemble des mathématiques sur une base axiomatique.
https://www.scientificamerican.com/article/what-is-godels-theorem/
https://plato.stanford.edu/entries/goedel-incompleteness/