Hilbert a donné les bases mathématiques nécessaires au développement de la mécanique quantique et de la relativité générale.
David Hilbert, mathématicien allemand (espaces de Hilbert, théorie des invariants, axiomatisation de la géométrie
David Hilbert (23 janvier 1862 [Königsberg] – 14 février 1943 [Göttingen]) est unanimement reconnu comme la figure emblématique des maths du XXe siècle. Son œuvre est immense, comparable à celle de Poincaré. Surtout, Hilbert a donné l’impulsion de nombreuses recherches mathématiques du XXe siècle et a créé une école allemande qui domina trente années durant. Hilbert est né le 23 janvier 1862 à Königsberg, d’une famille bourgeoise. Il fait sa thèse à l’université de la même ville, sous la direction de Lindemann, le mathématicien auquel on doit la première preuve de la transcendance de pi. 
C’est à cette époque qu’il se lie avec Minkowski, qui restera son ami toute sa vie. Les premiers travaux de Hilbert portent sur la théorie des invariants, qu’il aborde d’une façon radicalement nouvelle. Alors que ses prédécesseurs avaient obtenu des résultats partiels au prix de calculs lourds, il parvient à un résultat général – son fameux Nullstellensatz (en français théorème des zéros de Hilbert) – à l’aide de raisonnements abstraits. Il pose là les premières pierres de la géométrie algébrique abstraite, une thématique majeure du XXe siècle. Hilbert a donné les bases mathématiques nécessaires au développement de la mécanique quantique et de la relativité générale. En 1900, il propose au Congrès International des mathématiciens une liste de 23 problèmes, qui ont alimenté les recherches du 20ème siècle et dont tous n’ont pas encore été résolus.
Espaces de Hilbert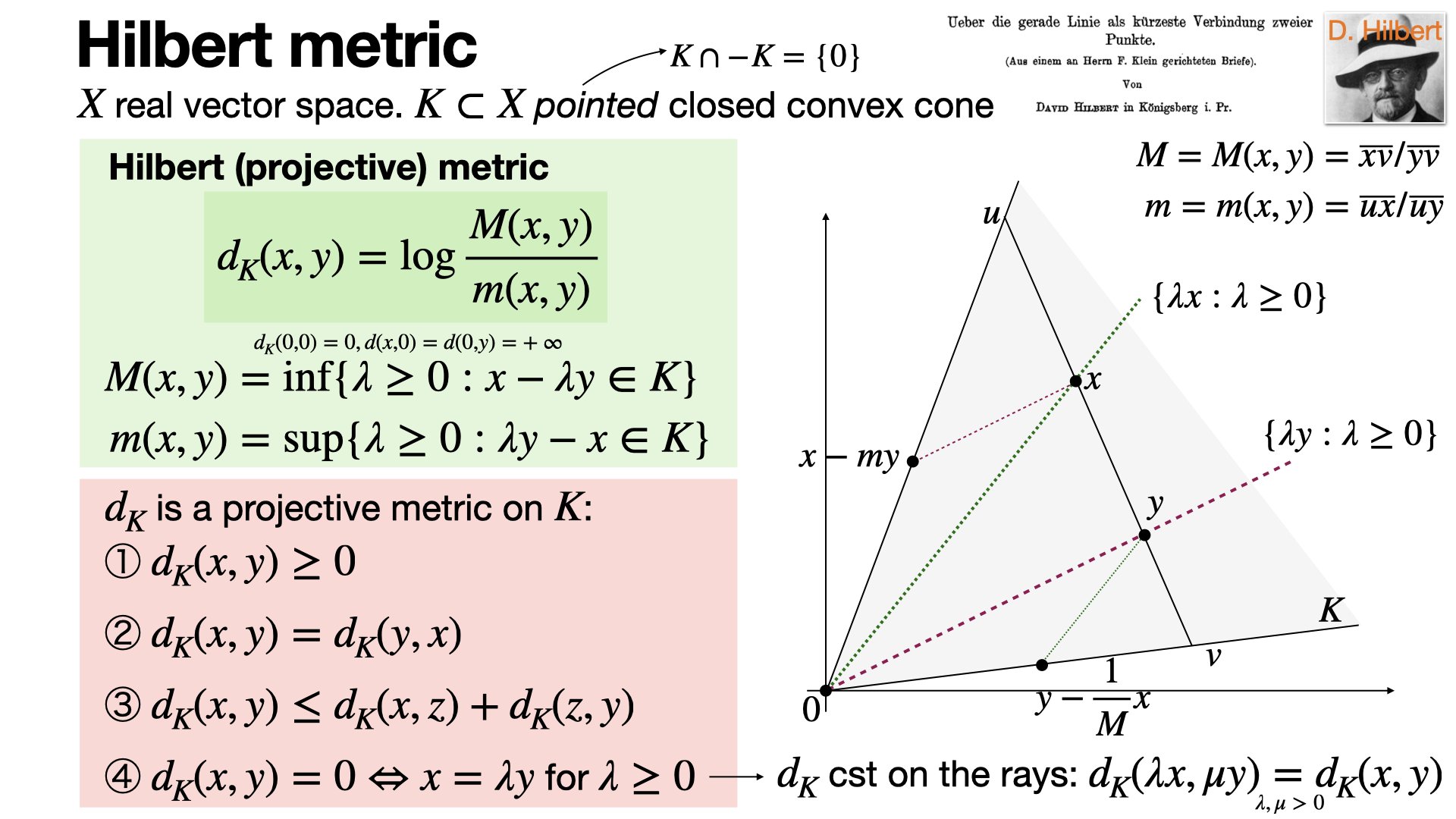 
Les espaces de Hilbert sont nés de l’intuition brillante du mathématicien David Hilbert, celle d’utiliser des méthodes géométriques dans le domaine de l’analyse. Prolongeant ainsi la notion d’espace euclidien, leur étude s’est révélée particulièrement fructueuse, notamment en mécanique quantique.
Décomposition de fonction
Il faut chercher l’origine du concept d’espace de Hilbert dans la question de la décomposition de fonction en séries de fonctions orthogonales. C’est le cas par exemple des séries de Fourier, qui permettent de décomposer des fonctions périodiques suivant des fonctions sinusoïdales. L’espace L2, l’espace des fonctions de carré intégrale, est un espace de Hilbert et est l’espace idéal pour une bonne théorie de Fourier. En effet, dans L2, toute fonction est somme de sa série de Fourier et toute série de Fourier pour somme une fonction L2 (ce résultat n’est pas vrai dans tous les espaces). La construction des espaces de Hilbert permet de décomposer des fonctions arbitraires en séries de fonctions orthogonales. Cette décomposition permet d’étudier des fonctions arbitraires (périodiques dans le cas de Fourier) de manière beaucoup plus simple. Cette possibilité s’appuie sur l’existence de bases de projection des éléments d’un espace de Hilbert, qu’il soit de dimension finie ou infinie.
La force de la théorie des espaces de Hilbert provient de l’introduction de méthodes géométriques au sein de l’analyse. Et notamment, de l’utilisation des concepts de produit scalaire, de norme, de base et de projection orthogonale. Ces espaces deviennent ainsi un prolongement naturel des espaces euclidiens dans le cas réel et hermitiens dans le cas complexe. Un produit scalaire est une application qui à deux éléments x et y de l’espace associe un réel ou un complexe et vérifiant certaines propriétés (linéarité en x, positivité, anti linéarité en y et nécessité d’être « définie », c’est-à-dire que le produit scalaire de x par x est nul si et seulement si x est nul). Un espace muni d’un produit scalaire est dit préhilbertien. Pour qu’il devienne un espace de Hilbert, il est nécessaire qu’il soit également complet, c’est-à-dire vérifiant une propriété sur les suites de Cauchy. Une fois l’espace muni d’un produit scalaire, on peut définir une norme et une notion de projection orthogonale.
Identité du parallélogramme
Une fois muni d’un produit scalaire, et donc d’une norme, un espace devient un espace de Hilbert et se trouve doté de propriétés similaires à celles de la géométrie classique dans des espaces euclidiens. Par exemple, les éléments d’un espace de Hilbert vérifient l’identité du parallélogramme. En géométrie euclidienne, cette identité affirme que la somme des carrés des longueurs d’un parallélogramme est égale à la somme des carrés de longueurs des diagonales. Cette propriété se retrouve dans les espaces de Hilbert et constitue même une condition nécessaire et suffisante pour être un espace de Hilbert. Ce résultat est connu sous le nom de théorème de Fréchet-von Neumann-Jordan. La géométrie dans un espace de Hilbert est ainsi très riche, avec l’inégalité de la médiane, l’inégalité de Cauchy-Schwartz ou encore les formules de polarisation, mais aussi la notion d’orthogonalité (deux éléments sont orthogonaux si leur produit scalaire est nul) et celle de projection sur une base hilbertienne.
Mécanique quantique
En mécanique quantique, diverses formulations ont été utilisées afin de décrire les états d’une particule. Ils sont, essentiellement, au nombre de trois : la mécanique ondulatoire, la mécanique matricielle et le formalisme invariant. Et le cadre commun à ces trois formalismes est justement les espaces de Hilbert. Si les deux premiers utilisent des espaces de Hilbert concrets, le formalisme invariant s’appuie lui sur un espace de Hilbert abstrait. La mécanique ondulatoire se construit dans l’espace L2 des fonctions de carré intégrable, les fonctions d’onde. De son côté, la mécanique matricielle s’appuie sur l’espace des suites de carré sommable, noté I2. L’espace de Hilbert utilisé pour le formalisme invariant, totalement abstrait, doit juste posséder une propriété supplémentaire, dite de séparabilité. C’est d’ailleurs en travaillant sur les fondements de la mécanique quantique que le physicien John von Neumann donnera la première définition axiomatique d’un espace de Hilbert en 1927.
En résumé
Les espaces de Hilbert sont apparus dans les travaux du mathématicien David Hilbert, ce dernier introduisant des méthodes géométriques dans des problèmes d’analyse mathématique. Ces espaces prolongent donc la notion d’espaces euclidiens. Ils sont ainsi dotés d’un produit scalaire, et donc d’une norme, d’une notion d’orthogonalité et de projections orthogonales sur une base (base hilbertienne). Outils très puissant, les espaces de Hilbert sont utilisés dans de très nombreux cas, notamment dans les diverses formalisations de la mécanique quantique.
Dans l’infini, il y a toujours de la place, dixit Hilbert 
Il n’y a là aucune erreur de raisonnement comme allait le montrer définitivement Georg Cantor en étendant d’une certain façon l’idée de Galilée dans le cadre de la théorie des ensembles qu’il a fondée avec son ami et collègue Richard Dedekind. Plus tard, au XXe siècle, plus précisément en 1947 dans un de ses ouvrages, le physicien George Gamow allait vulgariser l’infini de Cantor et ses paradoxes avec l’aide de « l’hôtel de Hilbert ». Il reprenait en fait un raisonnement déjà exposé par le grand mathématicien David Hilbert en 1924 comme l’explique dans un article sur arxiv l’éminent historien des sciences Helge Kragh. Mais qu’est-ce que l’hôtel de Hilbert ?
David Hilbert, mathématicien allemand (espaces de Hilbert, théorie des invariants, axiomatisation de la géométrie
Les travaux de Hilbert en géométrie ont eu la plus grande influence dans ce domaine après Euclide. Une étude systématique des axiomes de la géométrie euclidienne a conduit Hilbert à proposer 21 de ces axiomes et il a analysé leur signification. Il a apporté des contributions dans de nombreux domaines des mathématiques et de la physique.
David Hilbert était un bon exemple de mathématicien célèbre, établi et scrupuleux. Ses travaux ont contribué à ouvrir la voie à la recherche mathématique contemporaine. Il fut le tout premier à faire la distinction entre métamathématiques et mathématiques. Considéré comme l’un des meilleurs mathématiciens du XXe siècle, Hilbert a laissé un héritage de ses vastes connaissances dans diverses divisions des mathématiques et a également été la toute première personne à découvrir la théorie des invariants.
Premières années
David Hilbert est né en 1862 à Koenigsberg, en Prusse orientale. Il était le fils d’Otto Hilbert et de Maria. Alors que sa famille a survécu avec des moyens limités, son père était un juge réputé et sa mère était une passionnée d’astronomie et de philosophie. La mère de David était très fascinée par les formes et les nombres premiers et c’est potentiellement l’une des principales raisons pour lesquelles David excellait en mathématiques à un âge tendre. Il a également montré plus d’intérêt pour les langues, mais a abandonné cet intérêt pour se concentrer sur les mathématiques et les sciences.
Années d’études
David Hilbert est allé au Gymnase de Königsberg pour la première partie de ses études. Après avoir obtenu son diplôme là-bas, il est allé à l’Université de Königsberg pour étudier pour son doctorat, qu’il a obtenu en 1885. Parmi les amis de David à l’école se trouvait Minkowski, et ils se sont fortement influencés. Wallie Hurwitz a été nommé à l’Université de Königsberg en 1884 et il s’est également rapidement lié d’amitié avec David. Leur amitié a été un facteur très important dans les progrès mathématiques de David. David a obtenu son doctorat en philosophie de l’Université de Königsberg. Après avoir suivi les conseils de son ami Wallie Hurwitz pour explorer les mathématiques européennes, David a rencontré Felix Klein à Leipzig, Leopold Kronecker à Berlin et Henri Poincaré à Paris, seulement pour trouver leurs idées peu inspirantes.
Faits saillants de la carrière de Hilbert
Les premiers pas de la carrière de David ont eu lieu à l’Université de Göttingen lorsqu’on lui a proposé un poste de chargé de cours. Il a cependant refusé en raison du faible salaire. Il comptait sur les frais de ses élèves qui variaient selon le nombre d’étudiants qui assistaient à ses cours. David a eu du mal à continuer en tant que conférencier. Il a porté plainte à l’université. Quand David sentit que rien n’était fait pour améliorer la situation, il partit pour un autre voyage d’étude.
Comme sa dernière expérience n’était pas très bonne, cette fois-ci, David a planifié son voyage d’étude à l’avance pour rencontrer les plus grands mathématiciens du monde. Contrairement à son premier voyage, Hilbert était satisfait de son deuxième voyage et retourna à l’université pour travailler à la découverte de la solution à un problème mathématique sur des règles de base finie. Après plusieurs mois de travail acharné, David croyait avoir trouvé une solution parfaite au problème. Croyant que sa découverte était une percée mathématique, il est devenu fou de joie. David est resté à l’université en tant que chargé de cours de 1886 à 1892. L’Université de Göttingen était une tradition florissante en mathématiques principalement en raison des contributions de Carl Friedrich Gauss, Bernhard Riemann et Peter Gustav Lejeune Dirichlet au 19e siècle. Au cours des 30 premières années du XXe siècle, la tradition mathématique de l’école a atteint une plus grande éminence, principalement grâce à David Hilbert. L’Université de Göttingen a attiré des étudiants du monde entier.
Des années plus tard
Après sa percée réussie, David a également remporté de grands succès dans sa vie personnelle. Après que son ami Hurwitz soit devenu professeur à l’Ecole polytechnique fédérale de Suisse, David est devenu professeur assistant à l’Université de Königsberg. Quelques semaines plus tard, la Société mathématique allemande l’a chargé de mener une étude sur la théorie des nombres.
Les plus grands accomplissements
David Hilbert a découvert l’utilisation de l’algèbre et de la géométrie et il a eu l’idée des espaces de Hilbert. La découverte de Hilbert en géométrie a eu une énorme influence à cette époque. L’étude des axiomes de la géométrie euclidienne l’a amené à suggérer 21 de ces axiomes, dans lesquels il a examiné leur importance. Weyl, l’un des mathématiciens les plus influents de l’époque, appréciait ses travaux liés à une théorie des invariants et louait vivement l’engagement dont il faisait preuve envers le sujet.
Physique mathématique
Bien qu’il fût avant tout un mathématicien pur, Hilbert avait de larges goûts en mathématiques. Il y a peu ou pas de séparation entre les mathématiques appliquées et la physique mathématique. Hilbert s’est parfois essayé à ce domaine, souvent à la suite de discussions avec Hermann Minkowski, son vieil ami de l’époque où il était étudiant. Après avoir obtenu son diplôme, Minkowski a continué à enseigner à Albert Einstein à Zurich. En 1907, il reprend la théorie de la relativité restreinte d’Einstein, publiée en 1905, et montre qu’il peut être avantageux de la considérer différemment – dans un espace-temps à quatre dimensions – désormais appelé espace-temps de Minkowski. Peu à peu, une fascination pour la physique mathématique a grandi chez Hilbert, et il a passé de plus en plus de temps à réfléchir sur le sujet. En 1912, c’était devenu son principal domaine de recherche. Il croyait que la plupart des physiciens abordaient les problèmes avec une rigueur mathématique insuffisante. Il pensait que la physique bénéficierait de l’approche plus rigoureuse que les mathématiciens purs apportaient aux problèmes.
Les équations du champ gravitationnel de la relativité générale
À l’été 1915, Albert Einstein est venu à Göttingen à l’invitation de Hilbert pour donner une conférence pendant une semaine. Pendant des années, il avait lutté pour exprimer mathématiquement sa théorie générale de la relativité (encore) non publiée. La rencontre entre les deux grands esprits a évidemment été fructueuse, car en novembre, ils avaient indépendamment dérivé et publié des équations de champ de la gravitation, plaçant la théorie générale de la relativité d’Einstein sur une base mathématique solide. Hilbert et Einstein ont utilisé différentes méthodes pour trouver les équations – chaque méthode avait ses propres forces et faiblesses.
Hilbert n’a jamais revendiqué aucun crédit pour la découverte de ces équations, donnant le crédit à Einstein. Néanmoins, pour certaines applications, le traitement de Hilbert des équations de champ peut être plutôt utile.
Espace Hilbert
Hilbert a étendu l’algèbre vectorielle et le calcul afin qu’ils puissent être utilisés dans n’importe quel nombre de dimensions. Ce fut une énorme avancée dans le développement des mathématiques et de la physique. Aujourd’hui, Hilbert Space est incontournable en mécanique quantique, en analyse de Fourier et dans les applications des équations aux dérivées partielles, nombreuses en physique et en chimie physique.
Programme de Hilbert : la logique et les fondements des mathématiques
En 1920, Hilbert a fondé le formalisme mathématique. Il l’a fait après avoir réalisé qu’il y avait des incohérences au cœur de l’arithmétique. Il espérait répéter avec l’arithmétique et la théorie des nombres le succès qu’il avait connu en 1899 avec les axiomes de la géométrie. En choisissant les axiomes corrects, il espérait prouver que le reste des mathématiques classiques suivrait naturellement. En 1931, Kurt Gödel a prouvé que le programme de Hilbert ne pourrait jamais être pleinement réalisé. Les théorèmes d’incomplétude de Gödel ont prouvé qu’il existe des énoncés mathématiques qui, bien que vrais, ne peuvent jamais être prouvés mathématiquement.
La retraite de Hilbert
David Hilbert a pris sa retraite de son poste de professeur en 1930. Ses années de retraite ont été passées à vivre dans l’Allemagne nazie. Des mathématiciens juifs, dont beaucoup avaient été ses amis, furent bannis de Göttingen : ils partirent tous pour d’autres pays. Ce fut une fin triste et plutôt solitaire pour un mathématicien brillant, exceptionnellement influent, qui avait été l’ami de tout le monde et qui était connu pour sa joie de vivre. Lorsqu’il est arrivé pour la première fois en tant que nouveau professeur à Göttingen, il a bouleversé les professeurs plus âgés en se rendant à la salle de billard locale, où il a joué contre ses juniors. Il était vénéré par ses nombreux étudiants, avec qui il se faisait un devoir de se promener, afin qu’ils puissent parler de problèmes mathématiques de manière informelle. David Hilbert est décédé à l’âge de 81 ans le 14 février 1943 à Göttingen. Seulement une dizaine de personnes ont assisté à ses funérailles, un nombre pitoyable pour un grand mathématicien très aimé. Pour une raison ou une autre, les nazis avaient plus ou moins vidé la faculté de mathématiques de Göttingen des personnes que Hilbert connaissait. David Hilbert est enterré à Göttingen. Après la mort de Hilbert, Hermann Weyl, un ancien élève de Hilbert, qui a quitté l’Allemagne pour l’Amérique parce que sa femme était juive, a écrit : Aucun mathématicien de stature égale n’est sorti de notre génération… 
David Hilbert laisse dans le deuil son épouse Käthe Jerosch et son fils Franz. Franz avait une déficience intellectuelle et souffrait d’un ou plusieurs troubles mentaux. Il a passé quelque temps dans un hôpital psychiatrique. David Hilbert a eu du mal à accepter l’état de son fils. Käthe Jerosch est décédée en 1945 et Franz est décédé en 1969.
Bien que cette fin semble plutôt triste, Hilbert était un homme toujours optimiste quant à l’avenir de la culture et de la science humaines. Quand il était jeune homme, les croyances du physiologiste Emil du Bois-Reymond étaient en vogue. Du Bois-Reymond et ses partisans croyaient qu’il y avait des choses que les humains ne sauraient jamais. Ils pensaient qu’il y avait des limites à notre capacité à rassembler des connaissances scientifiques. Célèbre, ils ont dit : ignoramus et ignorabimus , ce qui signifie « nous ne savons pas et ne saurons pas ».
Hilbert a reçu de nombreuses distinctions. En 1905 , l’ Académie hongroise des sciences a décerné une citation spéciale à Hilbert. Il a reçu le prix Bolyai en 1910 et a été élu membre de la Royal Society of London en 1928 . En 1930 , Hilbert prit sa retraite et la ville de Königsberg le nomma citoyen d’honneur de la ville. Il a prononcé un discours qui s’est terminé par six mots célèbres montrant son enthousiasme pour les mathématiques et sa vie consacrée à la résolution de problèmes mathématiques :
David Hilbert (1862-1943)
https://mathshistory.st-andrews.ac.uk/Biographies/Hilbert/
https://www.famousscientists.org/david-hilbert/
https://totallyhistory.com/david-hilbert/
https://todayinsci.com/2/2_14.htm#death
https://www.bibmath.net/bios/index.php?action=affiche&quoi=hilbert
https://www.les-sciences.fr/sciences/les-espaces-de-hilbert/