Joseph Fourier est connu pour avoir déterminé, par le calcul, la diffusion de la chaleur en utilisant la décomposition de toute fonction en une série trigonométrique convergente![Calculating Fourier Coefficients using SCILAB [TUTORIAL] - YouTube](https://i.ytimg.com/vi/I3Hs0AUdf10/maxresdefault.jpg)
La vie du baron Jean Baptiste Joseph Fourier (1768-1830), physicien mathématicien, doit être considérée dans le contexte de la Révolution française et de ses répercussions. On pourrait dire que sa carrière a suivi les sommets et les creux de la vague politique.
Il a été tour à tour : professeur, policier secret, prisonnier politique, gouverneur d’Égypte, préfet de l’Isère et du Rhône, ami de Napoléon et secrétaire de l’Académie des sciences.
Mathématicien, égyptologue et administrateur français qui a exercé une forte influence sur la physique mathématique grâce à sa Théorie analytique de la chaleur (1822). Il a introduit une série mathématique infinie pour aider à résoudre les équations de conduction. Cette technique d’analyse permet de développer la fonction de n’importe quelle variable en une série de sinus de multiples de la variable, qui est maintenant connue sous le nom de série de Fourier. Ses équations ont donné naissance à de nombreux nouveaux domaines d’étude en mathématiques et en physique, y compris la branche de l’optique qui porte son nom, et ont ensuite été appliquées à d’autres phénomènes naturels tels que les marées, la météo et les taches solaires.
Son œuvre majeure, la Théorie analytique de la chaleur, a changé la façon dont les scientifiques conçoivent les fonctions et a réussi à énoncer les équations régissant le transfert de chaleur dans les solides.
Sa vie s’étend sur l’éclatement et les conséquences de la Révolution, la montée en puissance de Napoléon, sa défaite et son bref retour (les « Cent jours »), ainsi que la restauration des rois Bourbon.
Joseph Fourier est né en 1768 à Auxerre, dans le département de l’Yonne, une ville chargée d’histoire. Orphelin avant l’âge de dix ans, il grandit avec son oncle et sa tante dans la même ville. Sur la recommandation de l’évêque d’Auxerre, il est admis à l’École royale militaire voisine. Sous la direction de professeurs de l’ordre bénédictin, il se révèle être un élève rapide et assidu. Il étudie intensément les mathématiques. Dans le style des romans de l’époque, il est réputé avoir ramassé les bouts de bougies pour étudier tard dans la nuit, ruinant ainsi sa délicate constitution. Il est vrai qu’il était un enfant chétif selon les normes de l’époque, souffrant d’asthme et d’insomnie.
Ses professeurs voyaient en lui une recrue possible pour leur ordre. Pourtant, ce qu’il voulait vraiment, c’était entrer dans l’armée (dans l’artillerie ou le génie) : en raison de son origine modeste, son père était un simple tailleur, il en était empêché. Confondu, il choisit d’entrer dans l’Eglise. Il se rend alors à l’abbaye de Saint-Benoît-sur-Loire pour se préparer à prononcer ses vœux, tout en servant de professeur de mathématiques à ses camarades novices.
C’était en 1787. En arrière-plan, nous devons imaginer les premières vagues de mécontentement révolutionnaire qui commencent à assombrir la politique française.
La révolution de FourierFourier n’a jamais prononcé ses vœux. Il était prêt au faire, mais à peu près au même moment, un ordre de l’Assemblée constituante a mis un terme à la prise des ordres dans toute la France. On peut se demander si cela a été une déception pour lui. Quoi qu’il en soit, l’ordre nécessaire et la nature pratique de la vie monastique allaient exercer une forte influence sur l’œuvre de sa vie.
Fourier retourna travailler comme assistant de son ancien professeur de mathématiques, Bonard, à l’École Royale Militaire, plus tard le Collège National, à Auxerre. La congrégation de Saint-Maur, à laquelle appartiennent les professeurs, est exemptée de la répression révolutionnaire contre l’Église car il s’agit d’un ordre de jure.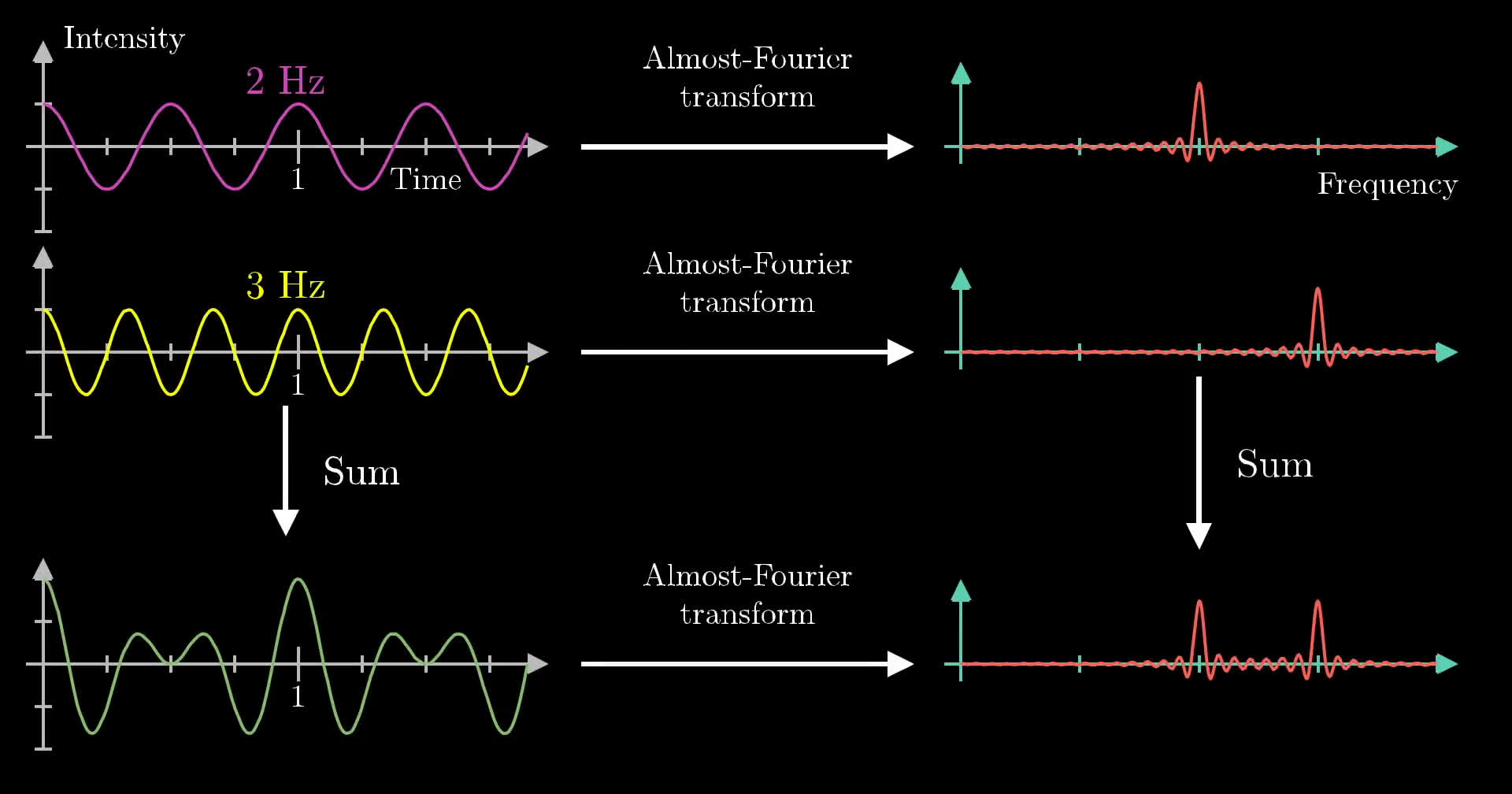
Sous la Commune, l’enseignement est rapidement réorganisé pour permettre l’accès à un plus grand nombre d’élèves. Il s’agissait de la poursuite, à la manière révolutionnaire, des réformes du Louis XVI déchu. Les historiens modernes considèrent les tentatives de Louis comme l’une des causes profondes de la Révolution. La combinaison d’une éducation améliorée et d’une récession continentale a laissé une grande population mécontente.
Fourier est resté à Auxerre pendant les quatre premières années de la Révolution. À cette époque, l’appel à la révolution ne pouvait raisonnablement pas être ignoré. Les idéaux élevés de ces premières années l’entraînent, mais plus tard, lorsque la France ressent la paranoïa de la Terreur, Fourier fait partie de ceux qui tentent de résister.
Une guerre commerciale faisait rage entre la Grande-Bretagne et la France. Lorsque la guerre inévitable est déclarée, le 1er février 1793, elle est populaire, du moins à Paris. L’appel à la révolution devient un appel aux armes sous la levée en masse de Carnot. Fourier s’adresse à la Société populaire d’Auxerre à ce sujet, insistant pour que les hommes levés soient de véritables volontaires. En raison de son éloquence, il est invité à rejoindre la société et est chargé d’organiser la levée dans la région. Cela signifie qu’il est élu au comité de surveillance, une organisation qui sera plus tard utilisée comme une force de police secrète. La municipalité lui confie d’autres missions importantes. L’une de ces missions lui vaut des ennuis.
À l’été de cette année-là, la France est en pleine tourmente ; la guerre à l’étranger est en recul et en Vendée, une contre-révolution royaliste bat son plein (ironiquement, en partie à cause de la résistance à la levée impopulaire). Fourier collectait des chevaux pour les deux efforts de guerre et, revenant d’une mission, passait par Orléans. À l’époque, c’était un foyer d’activité pour les sans-culottes. Par un concours de circonstances, les chefs des sans-culottes d’Orléans n’étaient pas appréciés par certains membres de la Convention, dont l’administrateur de la ville (un Montagnard – soutenant les bourgeois et l’avancement que leur argent pouvait apporter).
Dans cette atmosphère, Fourier parle au nom des dirigeants des sans-culottes de la ville. L’administrateur local se plaint à ses relations parisiennes et Fourier est finalement arrêté sous l’accusation d’être un Hébertiste, à une époque où Robespierre est de plus en plus paranoïaque quant aux autres clubs jacobins. Notre héros fut emprisonné pour n’être libéré qu’après le 9 thermidor (1794), date à laquelle Robespierre fut décapité.
En raison notamment des excès de la Terreur, au cours de laquelle de nombreux enseignants potentiels ont perdu la tête, il existe une volonté politique de créer un collège pour former de nouveaux enseignants. L’École Normale fut fondée dans ce but. Fourier fut désigné comme élève de la nouvelle école. Ce qui frappe le plus le lecteur moderne, ce sont les directives sur lesquelles l’école était dirigée : les conférences devaient être prononcées debout, sans notes préparées, les conférenciers devaient accepter les questions de l’assemblée lorsqu’elles se présentaient, et les conférenciers eux-mêmes devaient faire des recherches actives dans le domaine qu’ils enseignaient ! 
La première séance a lieu en janvier 1795. Fourier accepta avec empressement, peut-être parce que cela lui offrait la possibilité de quitter Auxerre pour les « grandes lumières » de Paris. Il y fait bon usage de son temps, dans la première moitié de 1795, et est certainement l’un des élèves les plus aptes à faire face à la classe de cours proposés. En septembre 1795, Fourier est à nouveau arrêté, à nouveau en relation avec les événements d’Orléans et son comportement ultérieur, cette fois-ci en tant que Robespierriste ! Ce deuxième emprisonnement semble avoir été le plus sérieux. Fourier écrit plus tard qu’il croyait vraiment qu’il allait mourir. Des amis et des collègues plaident en sa faveur. Une fois encore, ce sont des événements extérieurs qui le sauvent : après l’injection de grenades de Napoléon, une nouvelle amnistie est accordée et Fourier est libéré. Grâce aux relations qu’il avait nouées à l’École Normale, il devient professeur de mathématiques à l’École Centrale (qui deviendra plus tard l’École Polytechnique).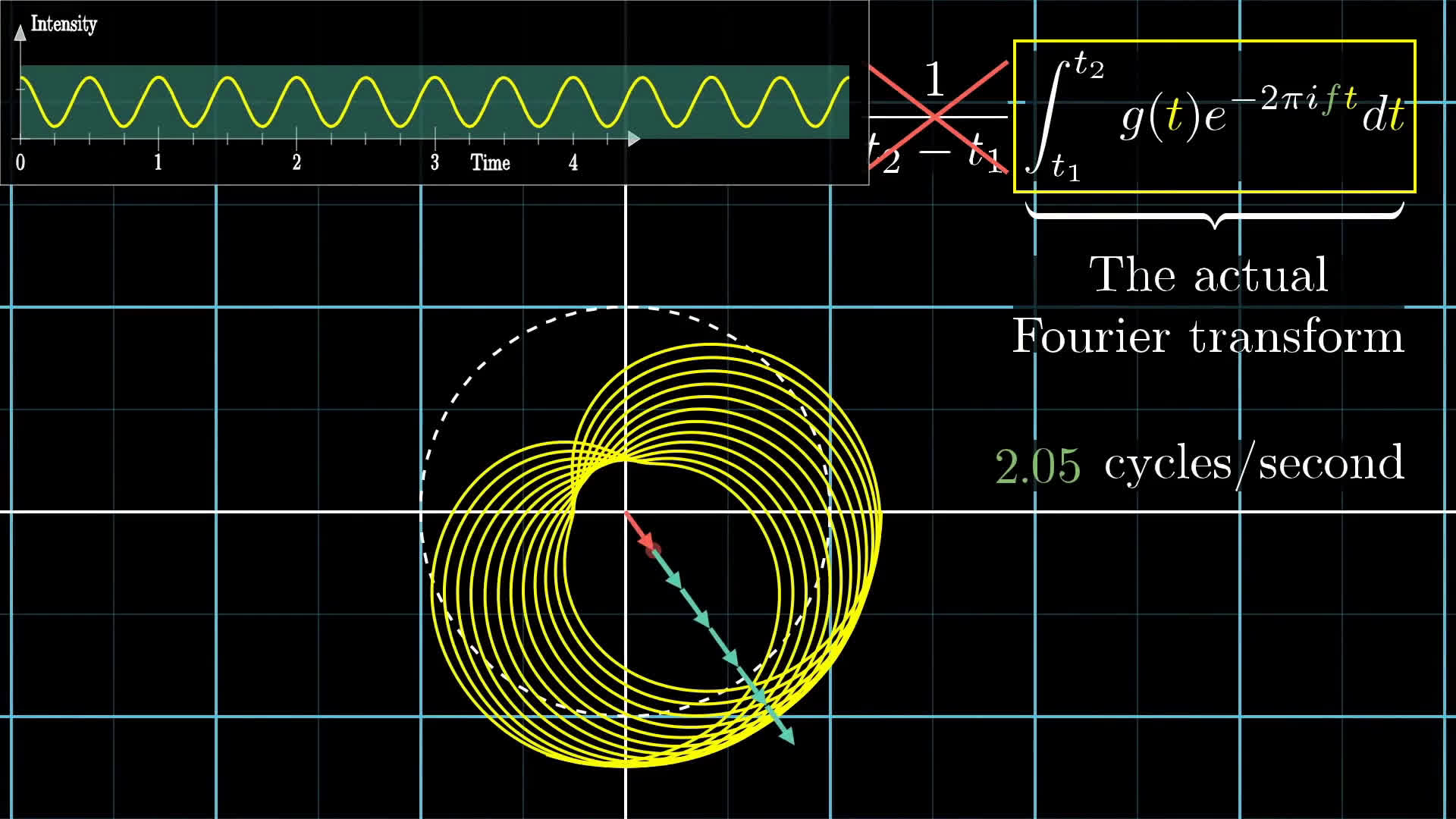
La campagne d’Égypte
Le 16 mai 1798, une armada de 180 navires appareille de Toulon. À bord se trouvent 30 000 soldats et marins, Napoléon Bonaparte, ses généraux et ses officiers, ainsi qu’un entourage de 165 scientifiques et littéraires, la « Légion de la culture », parmi lesquels Fourier. Leur destination n’est connue que de Napoléon et de quelques-uns de ses amis les plus sûrs.
Bien que Nelson, avec la flotte britannique, chasse la Méditerranée pour lui, Napoléon semble imperturbable, concentré sur la campagne à venir. Pour les équipages et les passagers, l’histoire est bien différente ; le stress est tangible.
C’est dans ce climat que Fourier a dû rencontrer Bonaparte pour la première fois. En tant que professeur à l’École polytechnique, Fourier faisait partie du personnel de Napoléon et était certainement impliqué dans les instituts. Il s’agit des soirées pour les officiers et les savants dont Napoléon est l’instigateur et auxquelles il participe. Fourier a presque certainement rencontré le général Kléber (le » bras droit » de Napoléon en Égypte).
Après la prise de Malte, la flotte poursuit sa route vers l’Égypte. La mission était désormais évidente : « libérer » le peuple égyptien de son « état inculte » brutal. L’armada débarque à Alexandrie, le 1er juillet 1798 (et la prend trois jours plus tard). Par la suite, la campagne a été marquée par de nombreux problèmes. Quelques jours seulement après avoir pris le Caire aux Marmelouks, la flotte française se saborde au large de la baie d’Aboukir. Les Français sont effectivement exilés ; de plus, le peuple qu’ils sont venus libérer ne semble pas apprécier leur présence !
Malgré tout, Napoléon (avec son esprit d’organisation) se met au travail pour améliorer la situation au Caire. Il forme le divan – une sorte de conseil municipal – en y incluant un observateur français (poste que Fourier occupera plus tard). Plus important encore pour Fourier, Napoléon crée l’Institut d’Égypte. Les préceptes fondateurs sont nobles : le développement des sciences en Égypte, la collecte de données historiques, statistiques, etc. et la recherche et le développement de l’armée. Ce dernier objectif était sûrement dû à Bonaparte lui-même.
La campagne d’Égypte s’essoufflant et les mauvaises nouvelles arrivant de chez lui, Napoléon rentre en France où il est élu Consul. Il confie le commandement de l’Égypte à Kléber. Ce fut de courte durée car Kléber ne s’est pas fait aimer des Égyptiens et a été assassiné. Fourier lit le discours des funérailles. Le nouveau commandant Menou connaissait le travail de Fourier à l’Institut et le fit mettre au Divan, parmi d’autres emplois de moindre importance, dont la somme faisait cependant de Fourier le gouverneur civil de l’Egypte.
Le harcèlement par le corps expéditionnaire britannique devient une menace en mars 1801 lorsque le général Abercrombie débarque dans la baie d’Aboukir. La défense française est dépassée à Alexandrie. Au Caire, les membres de l’Institut décident d’essayer de rentrer en France. Ils se rendent à Alexandrie, mais en quittant le port, leur navire est arrêté par le blocus britannique dirigé par Sir Sidney Smith.
Dans un geste caractéristique de l’époque, Sir Sidney donne aux savants un passage sûr jusqu’à Toulon (mais pas leur matériel de recherche). Fourier est de retour en France et il fait froid !
Peu après son retour, Napoléon lui écrit pour lui expliquer que le premier préfet de l’Isère, Ricard de Séalt, vient de mourir et que Fourier serait idéal pour le poste. Fourier a dû être mécontent ; il s’attendait à retrouver Paris et les discours scientifiques animés de savants de sa trempe. Aussi déçu soit-il, Fourier est plus malin que de refuser Bonaparte.
La préfecture (1802-1815)
Ricard n’avait pas laissé les affaires du département de l’Isère en bon ordre. L’administration (dont le centre est à Grenoble) est en désordre, si bien que Fourier doit s’occuper lui-même de presque tout. Il crée plusieurs postes, ce qui permet à nombre de ses amis de trouver un emploi dans la région. Fourier a de nombreuses responsabilités : en tant que préfet, il est à la fois un personnage public et un gouverneur. Les demandes d’informations statistiques du ministre de l’Intérieur (son supérieur immédiat) sont incessantes. Ces informations peuvent aller du prix des moutons au marché au nombre de dissidents connus et de membres de sectes religieuses. Le côté le plus sombre de son travail était la suppression de la littérature anti-gouvernementale et la censure du journal local.
On attend de lui qu’il s’occupe des questions diplomatiques qui concernent l’Isère ; il organise les visites du roi d’Espagne et du pape Pie VII dans la région, ainsi que celle de Napoléon.
En 1809, le gouvernement parisien fait pression pour que soit achevé le travail de recherche sur la campagne d’Égypte, que Fourier doit compiler. À un moment donné, Fourier effectuait des recherches, s’acquittait de ses responsabilités préfectorales et préparait la version définitive du rapport de l’Institut du Caire pour publication, la « Déscription de l’Égypte », tout cela en même temps. Il contourne ce problème en demandant des congés afin de terminer le travail égyptien. Il a certainement utilisé une partie de ce temps pour poursuivre ses expériences.
Il est décoré deux fois : une fois comme chevalier de la Légion d’honneur de Napoléon, en 1804, et à l’achèvement de la Déscription de l’Égypte, en 1809, comme baron (titre qui lui assure une bonne pension).
Ses principaux travaux publics furent l’assèchement d’une grande zone marécageuse à Bourgoin et la construction partielle d’une route vers Turin. Le premier projet peut sembler assez simple, mais comme il y avait de nombreux intérêts contradictoires entre les fermiers autour des terres, les paysans qui y vivaient et la noblesse locale, Fourier était obligé de rendre visite à pratiquement toutes ces personnes pour négocier leur coopération.
Une route directe vers Turin était une étape évidente maintenant que l’Italie avait été annexée. Fourier a finalement reçu la permission du ministre de l’Intérieur de construire cette route ; le ministre avait été sceptique au départ. Elle ne fut pas achevée sous Fourier en raison de l’abdication de Napoléon en avril 1814.
Cet événement place Fourier dans une situation difficile, car la route de l’exil de Napoléon sur l’île d’Elbe passe par Grenoble. Fourier écrit pour demander que la route soit changée, prétextant des troubles civils à Grenoble et le passage de Bonaparte qui provoquerait des troubles. Bien sûr, il voulait surtout éviter l’embarras de voir son ami vaincu. Il n’avait pas à s’inquiéter ; l’entourage de Napoléon n’est finalement pas passé par Grenoble.
Les circonstances sont différentes un an plus tard, lorsque Napoléon s’échappe de l’île d’Elbe. Cette fois, il se dirige directement vers Lyon par un itinéraire qui doit passer par Grenoble. Fourier est prévenu et prépare donc une défense symbolique de la ville à une porte et part par l’autre, en direction de Lyon (ostensiblement pour prévenir les Bourbons du danger). Il est ensuite revenu, pour être intercepté par les hommes de Napoléon. Napoléon est mécontent de la « désertion » de Fourier mais, se souvenant peut-être de sa propre désertion de son ami en Égypte, il donne à Fourier la préfecture du Rhône.
Lorsque Fourier se rendit compte de la nature vengeresse du gouvernement des Cent-Jours, il démissionna de ce poste. Napoléon est vaincu à Waterloo et envoyé en exil à Sainte-Hélène. Le bouleversement qui s’ensuit en France se reflète dans la vie de Fourier ; il perd sa baronnie, sa pension et sa réputation. En disgrâce et sans travail, il doit vendre beaucoup de ses biens personnels pour survivre. Les Bourbons, maintenant rétablis, excluaient de façon mesquine toute personne associée à Napoléon.
Finalement, Fourier se voit offrir un emploi au Bureau des statistiques du département de la Seine (y compris Paris) par le comte de Chabrol de Volvic : le préfet de ce département et un ami de Fourier par l’intermédiaire de l’École polytechnique et de l’Égypte. Cette somme lui permettait de vivre et de consacrer du temps à ses recherches.
Lors des élections ouvertes de l’Académie des sciences en 1816, Fourier remporte le vote ; le roi n’approuve cependant pas son adhésion. La prochaine occasion d’adhérer à l’Académie se présenta après la mort d’un membre, en 1817. Il remporte l’élection avec facilité. Cette fois, il n’y a pas d’objection. Il reste membre à vie.
Fourier s’était intéressé au phénomène de transfert de chaleur dès 1802. Il serait anecdotique de penser que son retour d’Égypte sur les côtes froides de la France en est la cause, bien que, d’après les récits de ses années en Isère, il soit concevable qu’il ait contracté un myxoedème en Égypte, une maladie qui rendrait la vie dans le froid des montagnes du Jura presque insupportable.
Il y a deux problèmes distincts dans toute description de la propagation de la chaleur : l’état d’équilibre (où une chaleur constante est fournie au corps concerné qui finit par atteindre une distribution équilibrée) ; et le refroidissement en fonction du temps d’un corps dans un air à température fixe.
Ses premières tentatives étaient de la nature d’un modèle abstrait : pas de transfert de chaleur en surface ; corps discrets ; et chaleur transférée par un mécanisme de navette du chaud au froid. En commençant par deux corps de masse égale (et de même matériau) et en ajoutant d’autres corps par la suite, il espérait généraliser encore davantage à n corps disposés en ligne droite, pour finalement fixer n à l’infini. Le modèle résultant n’était pas satisfaisant. Avec le recul, nous pouvons dire qu’il n’avait inclus aucun terme décrivant la raison pour laquelle la chaleur était conduite : il n’avait qu’un coefficient de conductivité ad hoc ! 
Il est resté bloqué jusqu’en 1804, date à laquelle Biot lui rend visite à Grenoble. Biot travaillait lui-même sur la propagation de la chaleur dans les solides et dans son travail, il a séparé le traitement du transfert de chaleur intérieur et des effets de surface. Plus important encore, son travail portait sur des corps continus. Avec ces indications, Fourier était bien placé pour commencer ses recherches. Le problème le plus simple de ce type était la barre mince (prisme), chauffée à une extrémité et refroidie à une température stable à l’autre. Ici, le modèle était unidimensionnel et le refroidissement de surface était toujours normal à la barre.
Le Mémoire
En décembre 1807, Fourier lit un long mémoire sur « la propagation de la chaleur dans les solides » devant la Classe de l’Institut de France. Il se concentre sur la diffusion de la chaleur entre des masses discrètes et certains cas particuliers de corps continus (barre, anneau, sphère, cylindre, prisme rectangulaire et cube).
L’équation de diffusion utilisée peut être énoncée en trois dimensions. L’article n’a jamais été publié car l’un des examinateurs, Lagrange, a dénoncé son utilisation de la série de Fourier pour exprimer la distribution initiale de la température.
Dans le cas de la barre mince, Fourier a utilisé la même méthode que dans son projet précédent. Il y utilisait encore la méthode des « tranches » pour dériver le flux. Plus tard (dans son essai de 1811 et dans son livre « Analytical Theory of Heat »), les tranches sont devenues des sections mathématiques, résolvant ainsi les difficultés liées à la description du flux thermique. Le problème était qu’en utilisant des tranches – bien qu’infiniment fines – il avait supposé un saut de température (la chaleur dans une tranche devait provenir de ses voisins immédiats). Cette hypothèse n’était pas réalisable physiquement (pas même en théorie) et constituait donc une faille majeure. L’introduction de sections mathématiques à la place des tranches a permis d’éviter ce problème. Malheureusement, les détracteurs (principalement Biot, Laplace et Poisson) ne semblaient pas être conscients de la signification de ce changement de « différence de température » à « gradient de température ». C’est l’une des critiques formulées à l’encontre des recherches de Fourier après 1807 (l’autre critique souvent formulée est la difficulté de la périodicité).
Les examinateurs ont fait remarquer que ses travaux ne rendaient pas justice à Euler et d’Alembert. Fourier le concède, mais il continue à affirmer que ses travaux sur les séries trigonométriques sont indépendants, puisqu’il n’a pas eu accès aux travaux mathématiques correspondants à Grenoble. Il est certain que son traitement de ces séries était original.Une omission qui lui a causé des problèmes concerne l’article de Biot de 1804. Il semble que Fourier ait envoyé à Biot une première copie de son mémoire : une copie qui ne faisait pas référence à la part de Biot dans le développement. Comme ils travaillaient tous deux dans le même domaine, il y avait une certaine rivalité. Se sentant lésé, Biot écrit une critique cinglante du mémoire de Fourier dans le « Mercure de France », un journal public. Fourier est indigné. Ils resteront ennemis tout au long de leur carrière et prendront un grand plaisir à déprécier les réalisations de l’autre.
En 1809, Poisson, un ami de Biot et un autre scientifique étudiant la propagation de la chaleur, écrit dans le Nouveau Bulletin des Sciences (dont il est le rédacteur) sur l’état des connaissances dans ce domaine. Il citait généreusement les travaux de Biot ; tandis que ses remarques sur les recherches de Fourier négligeaient délibérément les découvertes très considérables que Fourier avait faites dans les divers cas particuliers décrits dans son mémoire. L’ensemble de l’article semblait calculé pour insulter.
La recherche expérimentale
Après avoir traité le problème de la barre mince en 1804, cette dernière section commence par décrire l’anneau chauffé : en régime permanent puis en refroidissement.
Son équipement était basique mais efficace : un anneau de fer poli de ~30cm de diamètre maintenu en place par des supports en bois et chauffé par un brûleur Argand réglable. Six trous étaient percés à mi-chemin de l’anneau, dont quatre accueillaient des thermomètres sur l’échelle de Réamur (l’espace entre l’anneau et le thermomètre étant rempli de mercure – comme les deux autres trous). Pour atteindre l’état d’équilibre, un point de l’anneau a été chauffé tandis que le reste de l’anneau a été laissé libre de rayonner de la chaleur.
Pour le cas dépendant du temps, l’anneau a été placé à mi-chemin dans un four et ensuite retiré dans un bain isolant de sable. La distribution initiale était uniformément chaude autour d’une moitié et froide autour de l’autre. La courbe s’est ensuite aplatie au fur et à mesure que la chaleur passait du chaud au froid. La théorie de Fourier suggérait que, très vite, cette courbe se résorberait encore davantage pour donner un simple modèle sinusoïdal qui s’atténuerait progressivement jusqu’à ce que l’anneau soit à une température uniforme. Les expériences l’ont confirmé : les mesures étaient plus difficiles mais concluantes. Les petits écarts qui existaient étaient probablement dus à la nature peu fiable des thermomètres utilisés (les thermomètres, du type de ceux utilisés par Fourier, avaient tendance à être affectés par la pression atmosphérique tant dans leur fabrication que dans leur application).
Fourier a traité la distribution initiale des températures autour de l’anneau comme une superposition de nombreuses sinusoïdes simples qui variaient du pic au creux et au pic un nombre entier de fois le long de la circonférence de l’anneau. Il pensait que les sinusoïdes de plus haute fréquence s’amortissaient rapidement. Une sinusoïde avec une fréquence deux fois plus élevée impliquerait que la distance entre le pic chaud et le creux froid soit divisée par deux et qu’en plus, le gradient de température soit doublé. Par conséquent, une distribution sinusoïdale avec deux fois la fréquence s’amortirait quatre fois plus vite.
Parallèlement à son développement théorique, Fourier s’est ensuite attaqué à la vitesse expérimentale de refroidissement d’une sphère uniformément chauffée. Pour ce faire, il a chauffé une petite sphère en fer poli, puis l’a laissée refroidir. La sphère était spécialement percée pour que des mesures de thermomètre puissent être effectuées en son centre. Il a constaté que le fait de varier la méthode de chauffage avait peu d’effet, tandis que le fait de noircir la surface doublait approximativement la vitesse de refroidissement. Pour finir, il a comparé les taux de refroidissement d’un cube et d’une sphère (où le cube avait des côtés de la même longueur que le diamètre de la sphère). Pour ce faire, il a répété les expériences ci-dessus avec les deux solides dans les mêmes conditions.
Les résultats de ces deux expériences ne sont pas impressionnants : les erreurs expérimentales substantielles sont dues à des déficiences de l’équipement utilisé, en particulier des thermomètres.
Le prix
En 1810, l’Institut de France annonce que le Grand Prix de mathématiques de l’année suivante portera sur « la propagation de la chaleur dans les corps solides ». Le titre idéal pour Fourier. Le choix a certainement été influencé par les chicaneries politiques de Laplace et Monge, partisans de la cause de Fourier, et de Lagrange, un de ses détracteurs.
La Commission de juges fut nommée : Lagrange, Laplace, Malus, Haüy et Lacroix.
L’essai reprenait les dérivations de ses travaux précédents, tout en corrigeant de nombreux errata. Le seul changement majeur réside dans son traitement du flux, comme mentionné précédemment. En 1812, il reçoit le prix et les honoraires considérables qui l’accompagnent. Il a gagné le prix mais pas l’acclamation totale de ses arbitres. Ils reconnaissent que Fourier a les bonnes équations mais estiment que ses méthodes ne sont pas exemptes de difficultés.
Dans le cours normal des choses, l’essai qui lui a valu le prix serait maintenant publié. En raison de ses lourdes obligations préfectorales, il n’a pas pu voir cela se produire. Ce n’est qu’une fois rentré à Paris pour de bon qu’il a pu travailler à l’impression de ce qui était désormais « La théorie analytique de la chaleur ». Même dans ce cas, la théorie ne fut publiée qu’en 1822 (en raison de l’intransigeance de Delambre, alors secrétaire permanent de l’Institut – peut-être à la demande de Lagrange). Ce livre ne contenait que le côté analytique de l’essai de Fourier. Un volume complémentaire qui couvrirait son travail expérimental, les problèmes de chaleur terrestre et les questions pratiques (comme le chauffage efficace des maisons) ne fut jamais achevé. Le texte réel de son essai original est apparu en deux parties dans les Mémoires de l’Académie des Sciences en 1824 et 1826. Ce n’est qu’après que Fourier ait été élu secrétaire perpétuel.
La série de Fourier
Le germe de l’idée des séries de Fourier se trouve, avec le recul, dans les travaux de Léonard Euler. Euler s’intéressait à l’interpolation. Dans un problème ayant pour origine les perturbations planétaires, il a abordé et résolu des problèmes de la forme
f(x) = f(x-1) + F(x)
Les solutions étant les séries trigonométriques bien connues.
Euler, lui aussi, a produit l’expansion correcte du sinus de Fourier, mais à partir de sources erronées. Lagrange a fourni ce même résultat dans le contexte de la propagation des ondes sonores.
En 1754, d’Alembert, travaillant sur un problème astronomique, obtint un développement trigonométrique en cosinus pour l’inverse de la distance entre deux planètes en fonction de l’angle entre les vecteurs de l’origine aux planètes : c’est l’introduction de l’expression intégrale des coefficients de Fourier.
La signification réelle du concept de fonction a fait l’objet d’un grand débat. Avec de nombreuses séries trigonométriques infinies apparaissant dans une variété de situations, le décor était planté pour que Fourier innove en utilisant systématiquement les équations qui portent son nom.
Ces mêmes noms étaient associés à un autre problème de l’époque – la corde vibrante. Dès 1753, Bernoulli préconisait une solution en série trigonométrique, pour des raisons physiques. Alors qu’Euler et d’Alembert privilégient une solution fonctionnelle, malgré les problèmes à t = 0 (c’est-à-dire un coin dans une équation supposée différentiable). Euler ne pouvait pas accepter la solution de Bernoulli car il ne pouvait pas concilier la périodicité d’une telle série avec la non-périodicité évidente du problème physique. Il était certain que de telles séries trigonométriques ne pouvaient pas du tout représenter des fonctions non périodiques. Son erreur était son incertitude quant à la différence entre la généralité algébrique sur toute la ligne réelle et la généralité géométrique sur la longueur fixe de la corde. Fourier a résolu ce problème de périodicité en faveur de Bernoulli dans son mémoire de 1807.
Conclusion : La théorie analytique de la chaleur de Fourier a dérivé et justifié les équations de base de la propagation de la chaleur. Son impact est dû en partie au fait qu’elle ne s’inscrit pas dans le schéma de la « mécanique rationnelle et céleste », tout en conservant une simplicité mathématique.
De nature essentiellement mathématique, la nature exceptionnelle de l’ouvrage découle de son utilisation de l’analyse. Des équations différentielles partielles étaient utilisées pour représenter les phénomènes physiques, puis des conditions initiales et des conditions aux limites étaient appliquées, comme d’autres l’avaient fait dans de nombreux cas particuliers. Fourier est allé plus loin, il a fait la distinction entre les actions à l' »intérieur » et celles à la frontière d’une « surface » (exprimant chacune comme une équation séparée). Il a choisi librement les systèmes de coordonnées pour tirer parti des arguments de symétrie.
Il a ajouté des énoncés explicites des conditions initiales afin que le calcul explicite puisse être comparé au test expérimental.
Les techniques qu’il a utilisées n’auraient pas pu voir le jour sans sa contribution : aucun de ses contemporains n’était aussi sûr de l’utilisation de la séparation des variables ni aussi confiant dans les solutions en série infinie. La beauté de ces techniques était – et reste- leur large applicabilité.
Lorsque Victor Hugo a écrit dans Les Misérables :
Il y avait à l’Académie des Sciences un Fourier célèbre, que la postérité a oublié, et dans quelque mansarde un Fourier obscur, que l’avenir rappellera.
Il n’a pas eu le bénéfice de deux siècles de recul – son Fourier dans une mansarde est Charles Fourier, un philosophe politique. Une grande partie des mathématiques du XIXe siècle (et même du XXe siècle) doit beaucoup à la théorie analytique : les intégrales définies comme des sommes, la théorie des déterminants infinis et la convergence uniforme. Pour un travail qui était, au moins dans son esprit, physique, c’était et c’est toujours époustouflant. L’héritage de Joseph Fourier ne sera certainement pas oublié.
https://todayinsci.com/F/Fourier_Jean/FourierPoliticianScientistBio.htm