24 février 2001 – Claude Shannon mathématicien et père fondateur de la théorie de l’information

Claude Shannon, mathématicien américain et théoricien de l’information                                         Une théorie mathématique de la communication par Claude Shannon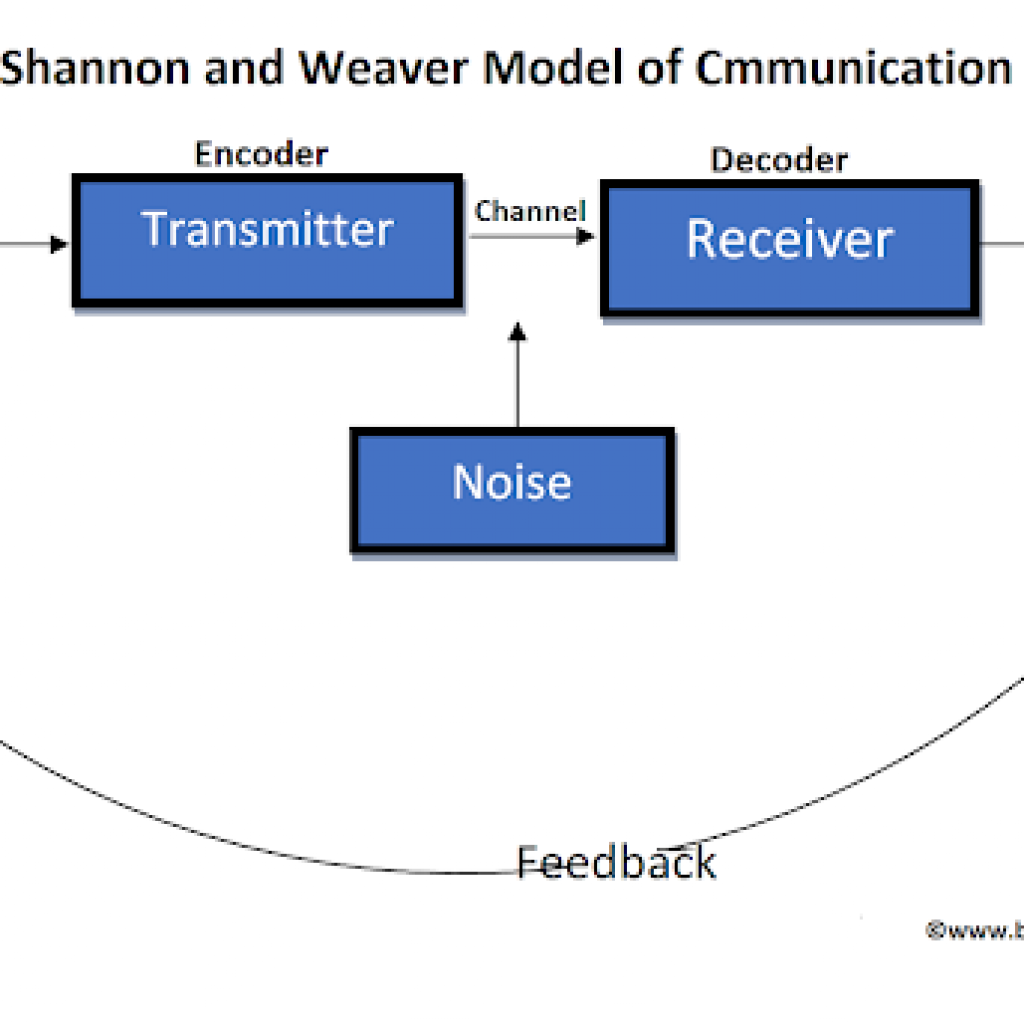Claude E. Shannon : fondateur de la théorie de l’informationClaude Shannon (1916-2001) est un ingénieur électricien et un mathématicien du XXe siècle, souvent considéré comme le père de la théorie de l’information. Il est né le 30 avril 1916 à Petoskey, dans le Michigan. Son père est un juge, et sa mère est le proviseur du lycée de Gaylord, une autre ville du Michigan. Il étudie à l’université du Michigan où il suit un double cursus en électricité et en mathématiques. Il obtient une licence dans ces deux disciplines en 1936, avant de poursuivre ses études au réputé MIT (Massachusetts Institute of Technology).Il soutient en 1940 une thèse de doctorat en mathématiques (elle portait sur des applications des mathématiques à la génétique) et un mémoire de master en électricité. Si la première fut largement ignorée, la seconde, qui explique comment utiliser les algèbres de Boole pour l’analyse des signaux électriques, est restée célèbre. En 1941, il est embauché dans les laboratoires de la compagnie de téléphone AT&T Bell. Immédiatement, il travaille sur des projets en liaison avec les services secrets, qui lui font notamment aborder des questions de cryptographie. En 1949, il se marie ; par la suite, il aura trois enfants.  Shannon travaille aux laboratoires de Bell jusqu’en 1971. Parallèlement à cela, il est aussi professeur au MIT de 1958 à 1978. Ses contributions essentielles concernent :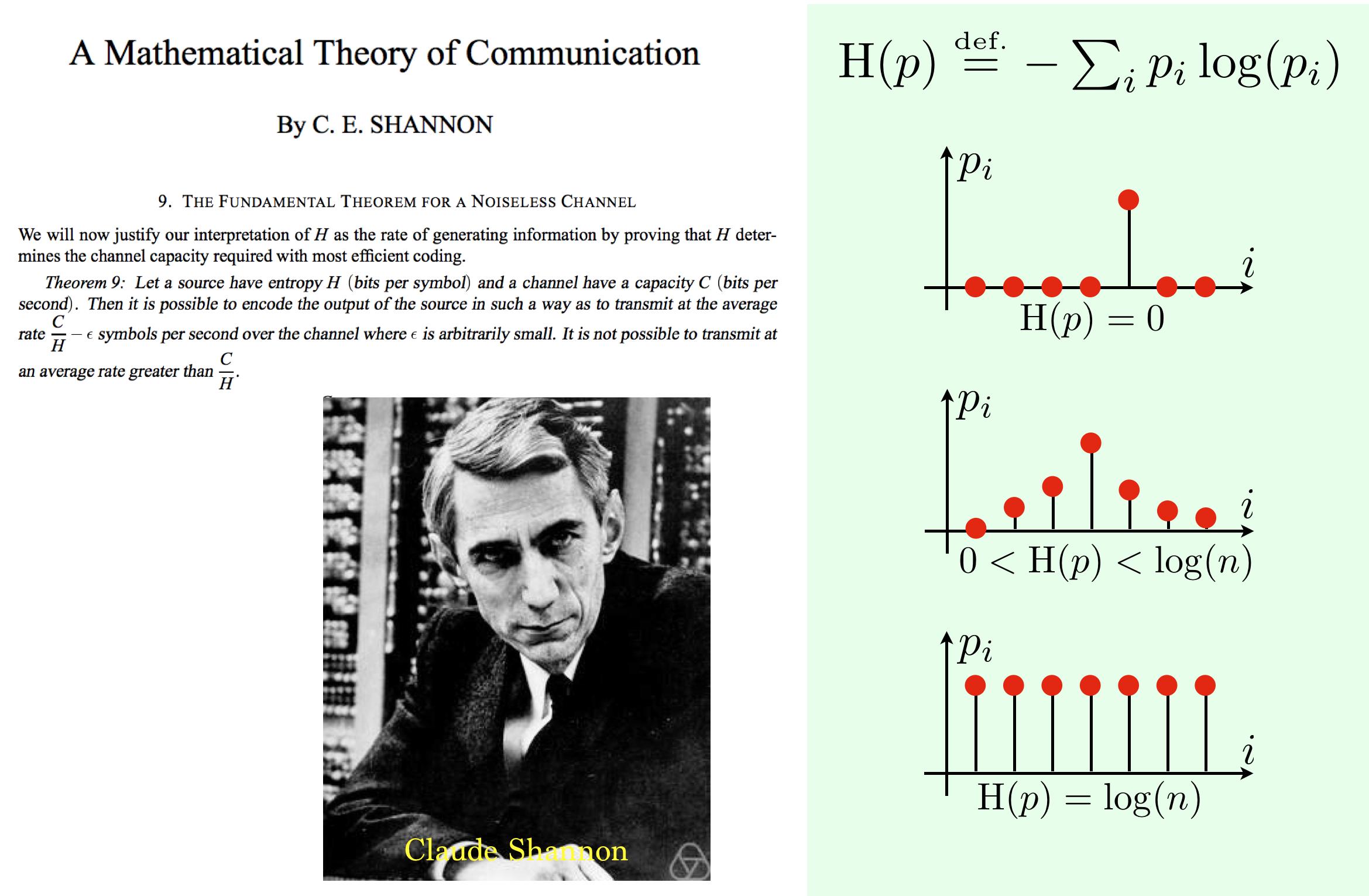-La théorie de la transmission des signaux; Shannon comprend que toute donnée, même la voix ou des images, peut se transmettre à l’aide d’une suite de 0 et de 1 (les bits), ouvrant la voie aux communications numériques et non plus analogiques. Il montre aussi comment le fait d’ajouter certains bits à un message peut permettre de vérifier que les autres ont été correctement transmis (on parle de code correcteur d’erreurs).

-L’entropie, qui mesure la quantité d’information portée par un message numérique ; cette notion est très importante en cryptographie ou en compression de données.-L’intelligence artificielle ; il conçoit par exemple le premier ordinateur qui joue aux échecs.

Shannon est aussi un personnage très original, connu pour déambuler dans les couloirs du MIT sur son monocycle tout en jonglant ! Il a reçu de nombreux honneurs, dont la médaille nationale des sciences des mains du Président Johnson en 1966, et le prix Kyoto en 1985. A la fin de sa vie, il souffre de la maladie d’Alzheimer, ce qui le conduit dans une maison de repos du Massachusetts. Il y décède le 24 février 2001, à l’âge de 84 ans.Claude Shannon est connu non seulement pour ses travaux dans les télécommunications, mais aussi pour l’étendue et l’originalité de ses hobbies, comme la jonglerie, la pratique du monocycle et l’invention de machines farfelues : une souris mécanique sachant trouver son chemin dans un labyrinthe, un robot jongleur, un joueur d’échecs (roi tour contre roi), etc.

Claude E. Shannon : fondateur de la théorie de l’informationAvec la nouvelle discipline fondamentale de la science de l’information quantique actuellement en construction, c’est le bon moment pour revenir sur un scientifique extraordinaire qui a lancé à lui seul la théorie classique de l’information

La science de l’information quantique est un domaine jeune, ses fondements étant encore posés par un grand nombre de chercheurs [voir « Règles pour un monde quantique complexe », par Michael A. Nielsen; Scientific American , novembre 2002 ]. La science de l’information classique, en revanche, est née il y a environ 50 ans, du travail d’un homme remarquable : Claude E. Shannon. Dans un article historique écrit aux Bell Labs en 1948, Shannon a défini en termes mathématiques ce qu’est l’information et comment elle peut être transmise face au bruit. Ce qui avait été considéré comme des modes de communication tout à fait distincts – le télégraphe, le téléphone, la radio et la télévision – ont été unifiés dans un cadre unique.Shannon est né en 1916 à Petoskey, Michigan, fils d’un juge et d’un enseignant. Entre autres efforts inventifs, dans sa jeunesse, il a construit un télégraphe de sa maison à celle d’un ami avec du fil de clôture. Il est diplômé de l’Université du Michigan avec des diplômes en génie électrique et en mathématiques en 1936 et est allé au MIT, où il a travaillé sous la direction du pionnier de l’informatique Vannevar Bush sur un ordinateur analogique appelé l’analyseur différentiel.

La thèse de maîtrise en génie électrique de Shannon au MIT a été qualifiée de la plus importante du XXe siècle: Shannon, 22 ans, a montré comment l’algèbre logique du mathématicien du XIXe siècle George Boole pouvait être mise en œuvre à l’aide de circuits électroniques de relais et de commutateurs. Cette caractéristique la plus fondamentale de la conception des ordinateurs numériques – la représentation du « vrai » et du « faux » et du « 0 » et du « 1 » sous forme d’interrupteurs ouverts ou fermés, et l’utilisation de portes logiques électroniques pour prendre des décisions et effectuer des calculs arithmétiques — peut être retracée aux idées de la thèse de Shannon.En 1941, avec un doctorat. en mathématiques à son actif, Shannon est allé aux Bell Labs, où il a travaillé sur des questions liées à la guerre, y compris la cryptographie. Inconnu de son entourage, il travaillait également sur la théorie de l’information et des communications. En 1948, ce travail a émergé dans un article célèbre publié en deux parties dans le journal de recherche de Bell Labs.

Quantification des informationsShannon a défini la quantité d’informations produites par une source – par exemple, la quantité dans un message – par une formule similaire à l’équation qui définit l’entropie thermodynamique en physique. Dans ses termes les plus élémentaires, l’entropie informationnelle de Shannon est le nombre de chiffres binaires nécessaires pour coder un message. Aujourd’hui, cela ressemble à un moyen simple, voire évident, de définir la quantité d’informations contenues dans un message. En 1948, à l’aube même de l’ère de l’information, cette numérisation de l’information de toute sorte était une étape révolutionnaire. Son article a peut-être été le premier à utiliser le mot «bit», abréviation de chiffre binaire.

En plus de définir les informations, Shannon a analysé la capacité d’envoyer des informations via un canal de communication. Il a découvert qu’un canal avait un certain taux de transmission maximal qui ne pouvait pas être dépassé. Aujourd’hui, nous appelons cela la bande passante du canal. Shannon a démontré mathématiquement que même dans un canal bruyant avec une faible bande passante, une communication essentiellement parfaite et sans erreur pouvait être obtenue en maintenant le débit de transmission dans la bande passante du canal et en utilisant des schémas de correction d’erreur : la transmission de bits supplémentaires qui permettraient au données à extraire du signal bruité.

Aujourd’hui, tout, des modems aux CD de musique, repose sur la correction d’erreurs pour fonctionner. Une réalisation majeure des scientifiques de l’information quantique a été le développement de techniques pour corriger les erreurs introduites dans l’information quantique et pour déterminer tout ce qui peut être fait avec un canal de communication quantique bruyant ou avec des bits quantiques intriqués (qubits) dont l’intrication a été partiellement dégradée. par le bruit.

● Entropie de Shannon ●L’entropie de l’information, souvent juste l’entropie, est une quantité de base dans la théorie de l’information associée à toute variable aléatoire, qui peut être interprétée comme le niveau moyen « d’information », « surprise » ou « incertitude » inhérente aux résultats possibles de la variable. Le concept d’entropie de l’information a été introduit par Claude Shannon dans son article de 1948 « Une théorie mathématique de la communication ». La définition de l’entropie utilisée dans la théorie de l’information est directement analogue à la définition utilisée en thermodynamique statistique. Cela se produit parce que Shannon a prouvé cette formule en utilisant la formule de l’entropie thermodynamique.Étant donné une variable aléatoire X, avec des résultats possibles xi chacun avec une probabilité P(xi), l’entropie H(X) de X est comme sur la photo. L’entropie de l’information est généralement mesurée en bits (également appelés « shannons »), correspondant à la base 2 dans l’équation ci-dessus. Il est aussi parfois mesuré en « unités naturelles » (nats), correspondant à la base e, ou en chiffres décimaux (appelés « dits », « bans » ou « hartleys »), correspondant à la base 10. L’idée de base de la théorie de l’information est que la « valeur informationnelle » d’un message communiqué dépend de la mesure dans laquelle le contenu du message est surprenant. Si un événement est très probable, il n’est pas surprenant (et généralement sans intérêt) que cet événement se produise comme prévu ; par conséquent, la transmission d’un tel message contient très peu d’informations nouvelles. Cependant, s’il est peu probable qu’un événement se produise, il est beaucoup plus instructif d’apprendre que l’événement s’est produit ou se produira.Par exemple, le fait de savoir qu’un numéro particulier ne sera pas le numéro gagnant d’une loterie fournit très peu d’informations, car tout numéro choisi particulier ne gagnera presque certainement pas. Cependant, savoir qu’un numéro particulier gagnera à la loterie a une grande valeur car il communique le résultat d’un événement à très faible probabilité. Voir moins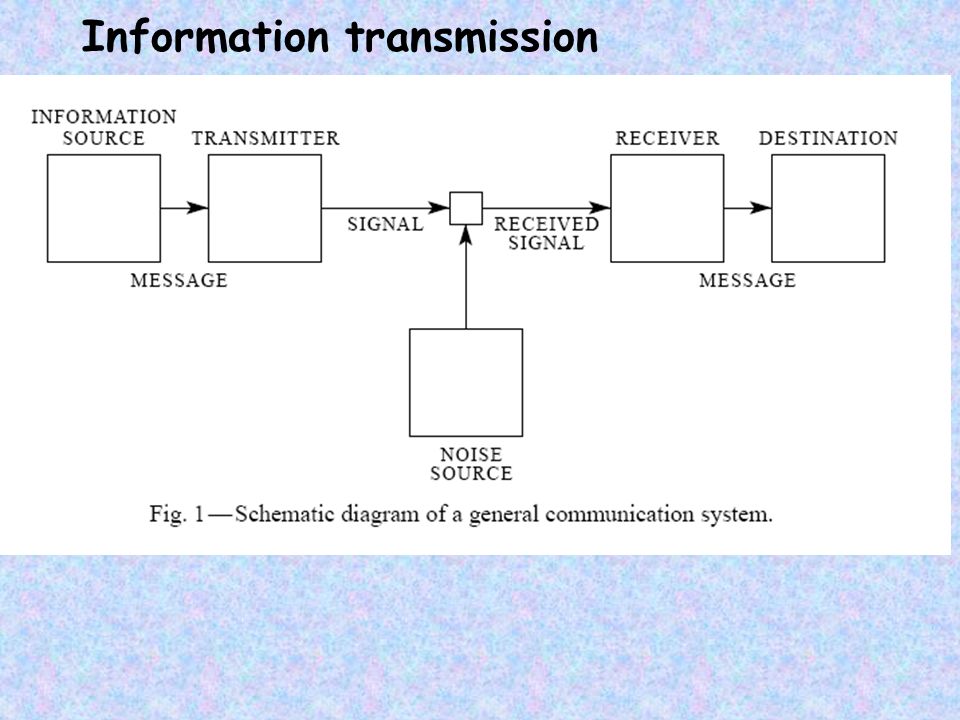Le code indéchiffrableUn an après avoir fondé et lancé la théorie de l’information, Shannon a publié un article qui prouvait qu’une cryptographie incassable était possible. (Il a fait ce travail en 1945, mais à ce moment-là, il était classé.) Le schéma s’appelle le tampon unique ou le chiffre Vernam, d’après Gilbert Vernam, qui l’avait inventé vers la fin de la Première Guerre mondiale. L’idée est pour encoder le message avec une série aléatoire de chiffres – la clé – de sorte que le message encodé soit lui-même complètement aléatoire. Le hic, c’est qu’il faut une clé aléatoire aussi longue que le message à encoder et qu’il ne faut jamais utiliser l’une des clés deux fois. La contribution de Shannon a été de prouver rigoureusement que ce code était incassable. À ce jour, aucun autre schéma de cryptage n’est connu pour être incassable.

Le problème avec le bloc à usage unique (soi-disant parce qu’un agent transporterait sa copie d’une clé sur un bloc et détruirait chaque page de chiffres après qu’ils ont été utilisés) est que les deux parties à la communication doivent chacune avoir une copie de la clé, et la clé doit être gardée secrète des espions ou des indiscrets. La cryptographie quantique résout ce problème. Plus correctement appelée distribution de clé quantique, la technique utilise la mécanique quantique et l’intrication pour générer une clé aléatoire identique à chaque extrémité du canal de communication quantique. La physique quantique garantit que personne ne peut écouter et apprendre quoi que ce soit sur la clé : toute mesure subreptice perturberait les corrélations subtiles qui peuvent être vérifiées, similaires aux vérifications de correction d’erreur des données transmises sur une ligne de communication bruyante.Le chiffrement basé sur le chiffrement de Vernam et la distribution de clé quantique est parfaitement sécurisé : la physique quantique garantit la sécurité de la clé et le théorème de Shannon prouve que la méthode de chiffrement est incassable.

Un génie du monocycle uniqueShannon a adapté le stéréotype du génie excentrique à un T. Aux Bell Labs (et plus tard au MIT, où il est revenu en 1958 jusqu’à sa retraite en 1978), il était connu pour rouler dans les couloirs sur un monocycle, jonglant parfois aussi. À d’autres moments, il sautillait dans les couloirs sur un pogo stick. Il a toujours été un amateur de gadgets et a notamment construit une souris robotique qui résolvait des labyrinthes et un ordinateur appelé le Throbac (« THrifty ROman-numeral BAckward-looking Computer ») qui calculait en chiffres romains. En 1950, il écrivit un article pour Scientific American sur les principes de la programmation d’ordinateurs pour jouer aux échecs .

Dans les années 1990, dans l’une des ironies tragiques de la vie, Shannon a contracté la maladie d’Alzheimer, qui pourrait être décrite comme la perte insidieuse d’informations dans le cerveau. Le canal de communication vers ses souvenirs – son passé et sa personnalité même – est progressivement dégradé jusqu’à ce que tous les efforts de correction d’erreur soient dépassés et qu’aucun signal significatif ne puisse passer. La bande passante tombe à zéro. L’extraordinaire modèle de traitement de l’information qu’était Claude Shannon a finalement succombé aux déprédations de l’entropie thermodynamique en février 2001. Mais une partie du signal généré par Shannon perdure, exprimé dans la technologie de l’information dans laquelle nos propres vies sont maintenant immergées.

https://www.bibmath.net/bios/index.php?action=affiche&quoi=shannon

https://www.universalis.fr/encyclopedie/claude-elwood-shannon/

https://www.scientificamerican.com/article/claude-e-shannon-founder/

https://journals.openedition.org/bibnum/1190