En 1872, un certain Edmund D. Barbour (1615-1685), de Boston, Massachusetts, a reçu deux brevets américains très intéressants pour des dispositifs de calcul (brevets américains №№ 130404 et 133188), décrivant une machine, qui semble être le premier représentant de ce qu’on appelle la multiplication directe. (Dans la même année 1872, Barbour a également reçu un brevet en Grande-Bretagne (GR187202437) et en France (Brevet N°96190). 
Dans son deuxième brevet, il a non seulement amélioré et simplifié sa première machine, mais a également fourni un mécanisme d’impression simple. De plus, en 1875, Barbour brevète une nouvelle machine (brevet US №168080), non pas à multiplication directe, mais avec un dispositif d’impression plus complexe. 
Barbour semble être l’un des premiers (après Müller et Babbage), qui a conçu un mécanisme d’impression pour sa calculatrice mécanique. Outre ces trois brevets, nous n’avons aucune autre information sur l’inventeur (Edmund D. Barbour, selon la demande de brevet) et si ses machines ont été fabriquées (très probablement elles n’avaient pas été commercialisées, à mon avis elles étaient trop avancées pour le moment). 
D’après mes recherches personnelles, l’inventeur était Edmund Dana Barbour (1841-1925), un homme d’affaires local de Boston, philanthrope et généalogiste, héritier (8e génération) de la glorieuse famille du capitaine George Barbour, le chef puritain de Dedham et Medfield, arrivés en Amérique en 1635 (voir biographie d’Edmund Dana Barbour). La plupart des premières machines à calculer effectuaient la multiplication comme une forme d’addition répétée. Pour multiplier, disons, par seize, on place le chariot dans sa position la plus à droite, on tourne six fois la manivelle de commande, on déplace le chariot d’une position vers la gauche et on tourne la manivelle une fois. Dans les machines à calculer à multiplication directe, l’opérateur n’avait qu’à effectuer opérations lorsque le multiplicateur était un nombre Digital.
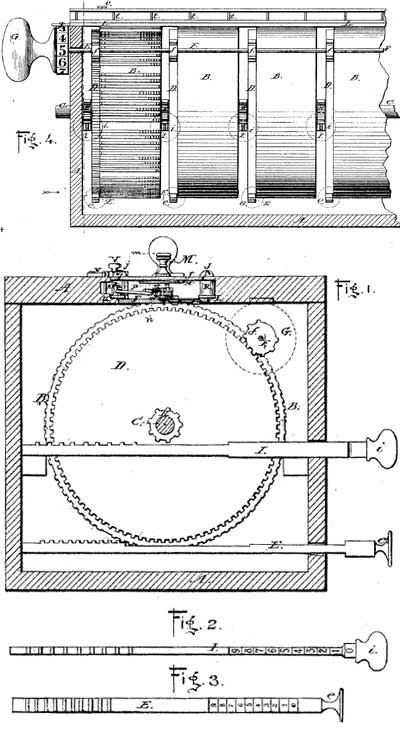
Les crémaillères employées par Barbour étaient nombreuses, une étant fournie pour chaque multiple des neuf chiffres, disposées en groupes constituant neuf ensembles montés sur les tambours marqués. Chacun de ces ensembles contient neuf crémaillères mutilées, dont la disposition des dents sert de multiple du chiffre qu’elles représentent.
En examinant attentivement le lecteur remarquera à partir des dessins que le plus bas des ensembles de crémaillères multiplicatrices montré sur le tambour, à gauche sur la Fig. 4, est la série d’une fois les neuf chiffres, le prochain ensemble ou série de racks ci-dessus sont les racks multiplicateurs pour les multiples de deux, le rack le plus bas de cette série n’ayant que deux dents, le suivant crémaillère supérieure à quatre dents, la crémaillère suivante à six et la suivante à huit. Jusqu’à présent, aucun multiple de deux n’a représenté plus d’une place ordinale d’unités, donc ces racks fonctionnent sur une roue numérique d’ordre inférieur et sont tous placés à droite du centre sur le tambour, mais le rack suivant au-dessus pour ajouter le multiple de deux fois cinq nécessite qu’un soit ajouté à un ordre supérieur, et est donc placé sur le côté gauche du centre du tambour.
Chacun des tambours est monté indépendamment sur l’arbre de pivot, et est fourni avec les crémaillères de réglage manuelles et, coopérant avec les engrenages et, pour aider à amener les crémaillères appropriées dans des positions engageables avec les pignons des roues numériques ou totales de l’accumulateur. Le pommeau, Fig. 4, et les engrenages, solidaires d’un arbre commun, fournissent un moyen d’actionner toute la série de tambours lorsque les bonnes séries multiples de crémaillères de chaque tambour ont été mises en place.
Comme exemple du fonctionnement de la calculatrice Barbour, supposons que 7894 doit être multiplié par 348. Le premier tambour à droite serait déplacé par ses racks de réglage jusqu’à ce que la série de racks multiplicateurs pour additionner les multiples de quatre soit présentée. , le tambour supérieur suivant à gauche serait réglé jusqu’à ce que la série de grilles de multiplication pour additionner les multiples de neuf soit présentée, le tambour supérieur suivant serait réglé pour les multiples de huit, et le tambour supérieur suivant, ou le quatrième à gauche, serait fixé pour les multiples de sept.
La crémaillère du tambour des milliers représentant le multiple de 8×7 présentera cinq dents pour la roue des dizaines de milliers et six pour la roue des milliers. Ainsi, en faisant glisser le chariot vers la droite d’un espace, les pignons des roues numériques engageront d’abord les dents des unités sur un tambour, puis les dents des dizaines sur le tambour inférieur suivant et amèneront les roues à enregistrer 63152. L’opérateur, en tournant le boutonau registre (4), le chiffre suivant du multiplicateur, tourne le tambour de sorte qu’une série de racks multiplicateurs représentant des multiples de 4 fois chaque chiffre du multiplicande soit présentée, de sorte qu’en faisant glisser le chariot d’un autre espace vers la droite, le multiple de 4×7894 seront ajoutés aux roues numériques. L’opérateur tourne ensuite le bouton pour enregistrer trois et déplace le chariot d’un espace supplémentaire vers la droite, ajoutant le multiple de 3 × 7894 aux roues de la série ordinale supérieure suivante, ce qui donne la réponse de 2747112.
Le modèle de l’US Patent Office (jusqu’en 1880, l’Office des brevets exigeait que les inventeurs soumettent un modèle avec leur demande de brevet) de la première machine à calculer d’Edmund D. Barbour est toujours conservé au National Museum of American History (voir la photo du haut). Le modèle breveté est une version très simplifiée de la machine brevetée, avec des dimensions globales : 14 cm x 41 cm x 13 cm. Il se compose de huit cylindres en bois qui tournent sur un arbre transversal à l’intérieur d’une boîte en bois. Chaque cylindre a autour de son bord 90 rangées de dents dentées (elles n’ont pas été réellement construites, seulement montrées comme des marques de stylo sur un bout de papier qui s’étend autour du premier cylindre). Chaque ensemble de neuf dents dentées représente les multiples d’un chiffre (les multiples de zéro correspondent à des espaces blancs).
La machine est réglée sur un multiplicateur donné en faisant tourner tous les cylindres avec un bouton à une extrémité de la machine (ce bouton manque également). Le premier cylindre a sur son côté gauche un engrenage droit en bois à 90 dents. Les autres cylindres auraient de tels engrenages, mais ils ne sont pas coupés. Tirer une crémaillère en bois sous l’engrenage l’avance d’un quatre-vingt-dixième de tour pour chaque unité sur la crémaillère. Par conséquent, l’opérateur peut définir un multiplicande. Un chariot mobile en laiton sur le dessus de la machine est censé être lié aux cylindres, de sorte que lorsque le chariot est tiré d’une unité vers la droite, les roues d’enregistrement avancent proportionnellement à la figure représentée sur le bord des cylindres (dans le modèle, les vérins ne sont pas liés au chariot coulissant).
Machine à calculer
En 1872, le premier brevet américain pour une machine à additionner capable d’imprimer des totaux et des sous-totaux, appelée « machine à calculer », fut délivré à E.D. Barbour de Boston, Mass. Cependant, ce n’était pas pratique. (N° 133 188)