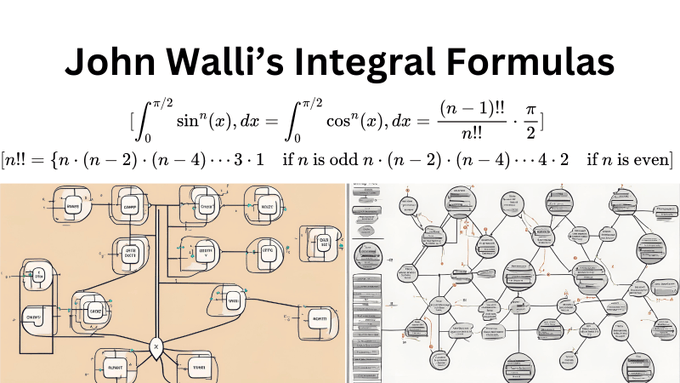
En utilisant le concept de continuité de Kepler, i John Wallis l a découvert des méthodes pour évaluer les intégrales.
John Wallis (1616-1703) était un mathématicien anglais qui s’appuya sur la méthode des indivisibles de Cavalieri pour concevoir une méthode d’interpolation. En utilisant le concept de continuité de Kepler, il a découvert des méthodes pour évaluer les intégrales.
John Wallis était un mathématicien anglais né le 23 octobre 1616 à Ashford, dans le Kent. Il a fait ses premières études dans une école locale d’Ashford, mais il a ensuite été transféré à l’école de James Movat à Tenterden en 1625 après une épidémie. Cependant, les mathématiques sont devenues une partie importante de sa vie après avoir commencé à les étudier à l’école de Martin Holbeach à Felsted. Son premier choix de carrière était d’être médecin pour lequel il a même été envoyé à l’Emmanuel College de Cambridge, mais ses intérêts pour les mathématiques dépassaient son premier choix. Wallis a obtenu un baccalauréat en art en 1637 et une maîtrise en 1640. Il est devenu prêtre en 1643 et a continué à servir à l’Assemblée de Westminster jusqu’en 1649. Il a ensuite été élu membre du Queen’s College de Cambridge. Wallis était également impliqué dans la politique actuelle de l’époque.
Les contributions de Wallis dans de nombreuses branches des mathématiques sont d’une grande importance. Il a fait des progrès dans la trigonométrie, la géométrie et le calcul. Il est également crédité pour l’analyse de la série infinie. Il a fait de nombreuses innovations telles que l’introduction du terme «fraction continue» et l’utilisation du symbole de l’infini pour la première fois. On dit aussi qu’il est l’initiateur de la droite numérique
Wallis a également travaillé sur la statique en 1669 et sur la dynamique en 1670. On dit que c’est Wallis qui a donné la preuve du théorème de Pythagore avec l’utilisation de triangles similaires, mais ce n’est pas un fait confirmé. Wallis avait une autre compétence et c’était de faire des calculs mentaux. Il calculait de grands nombres dans sa tête et s’en souvenait même l’autre jour. Cela a été considéré comme une telle réussite qu’il a même été discuté dans les » Transactions philosophiques » de la Royal Society en 1685.
Wallis a également travaillé en physique, théologie, étymologie, philosophie générale, pédagogie et linguistique. Il a reçu le poste de professeur savilien de géométrie à Oxford, poste qu’il a occupé à vie. Il mourut le 28 octobre 1703 après avoir inspiré de nombreuses personnes par ses formidables contributions aux mathématiques.
Il a été nommé à la chaire savilienne de géométrie à Oxford en 1649 par Cromwell principalement en raison de son soutien aux parlementaires. Certes, l’ancien titulaire de la chaire, Peter Turner, a été renvoyé pour ses opinions royalistes. Cromwell tenait Wallis en haute estime, non seulement pour ses opinions politiques, mais aussi pour son érudition. Wallis a occupé la chaire savilienne pendant plus de 50années jusqu’à sa mort et, même s’il a été nommé pour de mauvaises raisons, il méritait assurément d’occuper le fauteuil. Ce n’était pas le seul poste que Wallis occuperait à Oxford. En 1657, il est nommé conservateur des archives de l’Université. Il y avait une controverse considérable sur son élection à ce poste.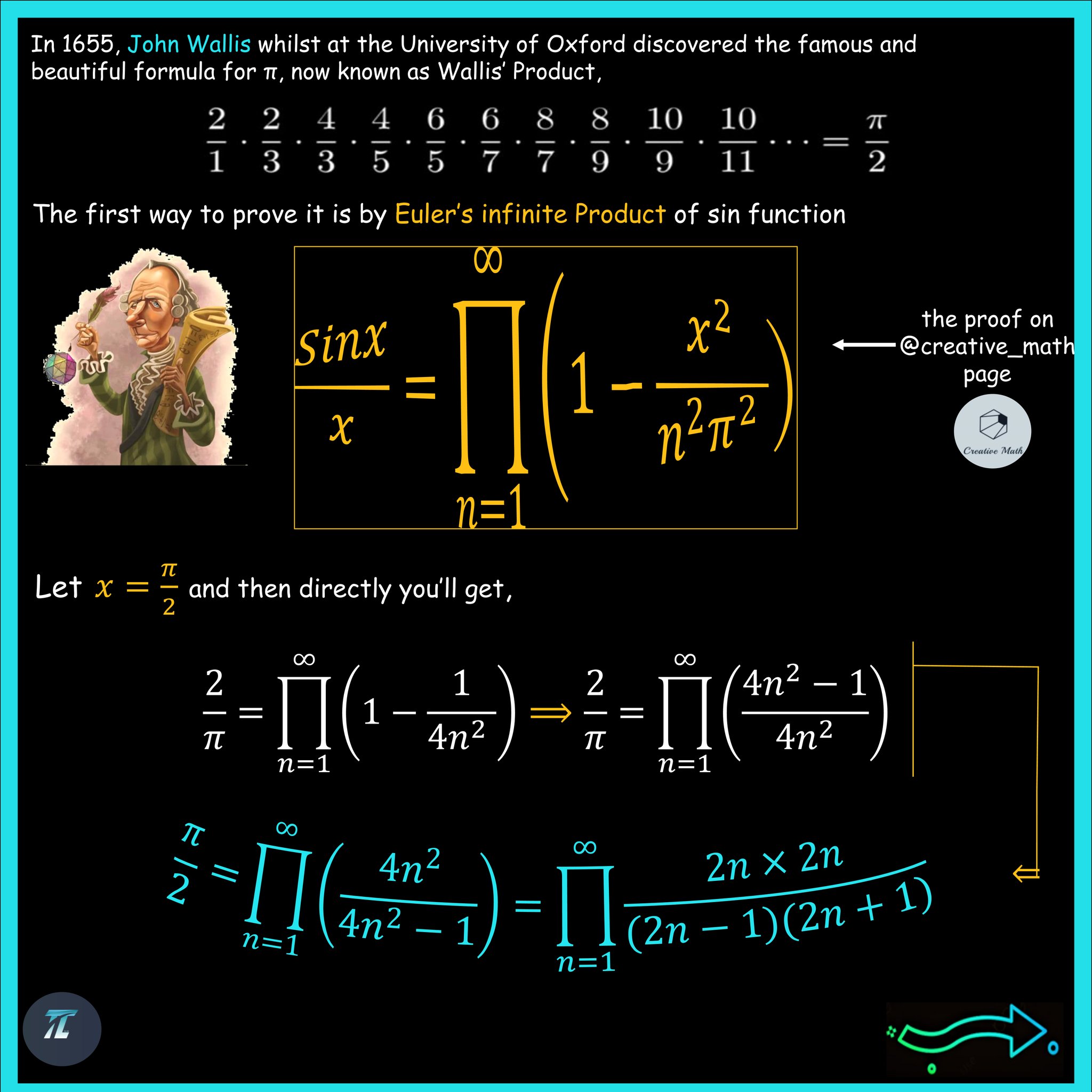
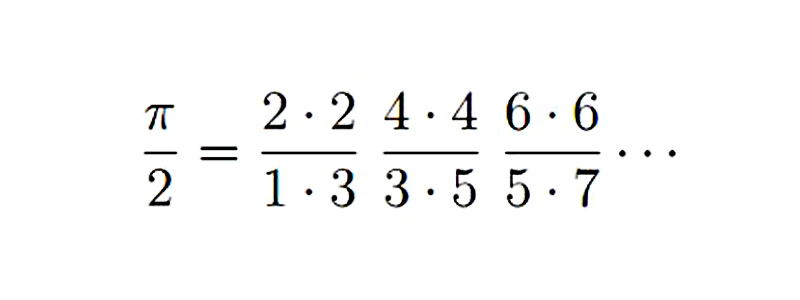
Wallis est devenu impliqué dans une dispute amère avec Hobbes, qui bien qu’un bon érudit, était bien en dessous de la classe de Wallis en tant que mathématicien. En 1655, Hobbes prétend avoir découvert une méthode pour quadriller le cercle. Le livre de Wallis Arithmetica infinitorum avec ses méthodes était sous presse à l’époque et il a réfuté les affirmations de Hobbes
Les symboles de la communication en mathématiques
Symbole, un élément de communication destiné à simplement exprimer ou représenter un complexe de personne, d’objet, de groupe ou d’idée. Les symboles peuvent être représentés graphiquement, comme dans la croix pour le christianisme et la croix rouge ou le croissant pour les organismes de préservation de la vie des pays chrétiens et islamiques (voir Croix-Rouge et Croissant-Rouge ; représentationnellement, comme dans les figures humaines Marianne, John Bull et Oncle Sam représentant respectivement la France, l’Angleterre et les États-Unis ; ils peuvent impliquer des lettres, comme dans K pour l’élément chimique potassium ; ou ils peuvent être attribués arbitrairement, comme dans le symbole mathématique ∞ pour l’infini ou le symbole $ pour le dollar .
Dans divers contextes philosophiques et particulièrement en sémiotique, une branche de la métalogique, des distinctions très précises sont faites entre symbole et signe.
Calcul
Calcul, branche des mathématiques concernée par le calcul des taux de variation instantanés (calcul différentiel) et la sommation d’une infinité de petits facteurs pour déterminer un ensemble ( calcul intégral ). Deux mathématiciens, Isaac Newton d’Angleterre et Gottfried Wilhelm Leibniz d’Allemagne, partagent le mérite d’avoir développé indépendamment le calcul au 17ème siècle. Le calcul est désormais le point d’entrée de base pour quiconque souhaite étudier la physique, la chimie, la biologie, l’économie, la finance ou l’actuariat. Le calcul permet de résoudre des problèmes aussi divers que suivre la position d’une navette spatiale ou prédire la pression qui s’accumule derrière un barrage lorsque l’eau monte. Les ordinateurs sont devenus un outil précieux pour résoudre des problèmes de calcul qui étaient autrefois considérés comme incroyablement difficiles.
Calcul des courbes et des aires sous les courbes
Les racines du calcul se trouvent dans certains des problèmes de géométrie les plus anciens jamais enregistrés. Le papyrus égyptien Rhind (vers 1650 av. J.-C.) donne des règles pour trouver l’aire d’un cercle et le volume d’une pyramide tronquée. Les géomètres de la Grèce antique ont cherché à trouver des tangentes aux courbes, le centre de gravité des figures planes et solides et les volumes d’objets formés en faisant tourner diverses courbes autour d’un axe fixe.
En 1635, le mathématicien italien Bonaventura Cavalieri avait complété les outils rigoureux de la géométrie grecque par des méthodes heuristiques qui utilisaient l’idée de segments infiniment petits de lignes, d’aires et de volumes. En 1637, le mathématicien et philosophe français René Descartes publia son invention de la géométrie analytique pour donner des descriptions algébriques de figures géométriques. La méthode de Descartes, associée à une idée ancienne de courbes générées par un point en mouvement, a permis à des mathématiciens tels que Newton de décrire le mouvement de manière algébrique. Du coup, les géomètres purent dépasser les cas isolés et les méthodes ad hoc d’autrefois. 
Calcul des vitesses et des pentes
Le problème de trouver des tangentes aux courbes était étroitement lié à un problème important qui découlait des recherches sur le mouvement du scientifique italien Galileo Galilei, celui de trouver la vitesse à tout instant d’une particule se déplaçant selon une loi. Galileo a établi qu’en t secondes, un corps en chute libre tombe sur une distance gt²/2, où g est une constante (plus tard interprétée par Newton comme la constante gravitationnelle). Avec la définition de la vitesse moyenne comme la distance par temps, la vitesse moyenne du corps sur un intervalle de t à t + h est donnée par l’expression [g(t + h)²/2 – gt²/2]/h. Cela se simplifie en gt + gh/2 et s’appelle le quotient de différence de la fonction gt²/2. Lorsque h se rapproche de 0, cette formule se rapproche de gt, qui est interprété comme la vitesse instantanée d’un corps tombant au temps t.
Différenciation et intégration
Indépendamment, Newton et Leibniz ont établi des règles simples pour trouver la formule de la pente de la tangente à une courbe en tout point de celle-ci, étant donné uniquement une formule pour la courbe. Le taux de variation d’une fonction f (notée f′) est appelé sa dérivée. Trouver la formule de la fonction dérivée s’appelle la différenciation, et les règles pour ce faire forment la base du calcul différentiel. Selon le contexte, les dérivées peuvent être interprétées comme des pentes de lignes tangentes, des vitesses de particules en mouvement ou d’autres quantités, et c’est là que réside la grande puissance du calcul différentiel.
Une application importante du calcul différentiel est la représentation graphique d’une courbe étant donné son équation y = f(x). Il s’agit notamment de trouver des points maximum et minimum locaux sur le graphe, ainsi que des changements d’inflexion (convexe à concave, ou inversement). Lors de l’examen d’une fonction utilisée dans un modèle mathématique, ces notions géométriques ont des interprétations physiques qui permettent à un scientifique ou à un ingénieur de se faire rapidement une idée du comportement d’un système physique.
L’autre grande découverte de Newton et Leibniz était que la recherche des dérivées des fonctions était, dans un sens précis, l’inverse du problème de la recherche des aires sous les courbes – un principe maintenant connu sous le nom de théorème fondamental du calcul. Plus précisément, Newton a découvert que s’il existe une fonction F(t) qui désigne l’aire sous la courbe y = f(x) de, disons, 0 à t, alors la dérivée de cette fonction sera égale à la courbe d’origine sur cet intervalle, F′ (t) = f(t). Ainsi, pour trouver l’aire sous la courbe y = x² de 0 à t, il suffit de trouver une fonction F telle que F′(t) = t2. Le calcul différentiel montre que la fonction la plus générale de ce type est x**3/3 + C, où C’est une constante arbitraire. C’est ce qu’on appelle l’intégrale (indéfinie) de la fonction y = x², et elle s’écrit ∫x²dx. Le symbole initial ∫ est un S allongé, qui signifie somme, et dx indique un incrément infiniment petit de la variable, ou axe, sur lequel la fonction est sommée. 
Leibniz a introduit cela parce qu’il considérait l’intégration comme la recherche de l’aire sous une courbe par une sommation des aires d’une infinité de rectangles infiniment minces entre l’axe des x et la courbe. Newton et Leibniz ont découvert que l’intégration de f(x) équivaut à résoudre une équation différentielle — c’est-à-dire trouver une fonction F(t) telle que F′(t) = f(t). En termes physiques, la résolution de cette équation peut être interprétée comme la recherche de la distance F(t) parcourue par un objet dont la vitesse a une expression donnée f(t). La branche du calcul concernée par le calcul des intégrales est le calcul intégral, et parmi ses nombreuses applications, on trouve le travail effectué par des systèmes physiques et le calcul de la pression derrière un barrage à une profondeur donnée.
Infinitésimal, en mathématiques
Infinitésimal, en mathématiques, une quantité inférieure à toute quantité finie mais non nulle. Même si une telle quantité ne peut exister dans le système des nombres réels, de nombreuses premières tentatives pour justifier le calcul étaient basées sur un raisonnement parfois douteux sur les infinitésimaux : les dérivées étaient définies comme des rapports ultimes d’infinitésimaux, et les intégrales étaient calculées en additionnant des rectangles de largeur infinitésimale. En conséquence, le calcul différentiel et intégral était à l’origine appelé calcul infinitésimal. Cette terminologie a progressivement disparu au fur et à mesure que des concepts rigoureux de limite, de continuité et de nombres réels ont été formulés.
John Wallis (1616-1703)
Mathématicien britannique qui a introduit le symbole mathématique de l’infini. Wallis était doué en cryptographie et décodait les messages royalistes pour les parlementaires pendant la guerre civile. Par la suite, il fut nommé à la chaire savilienne de géométrie à Oxford en 1649, poste qu’il occupa jusqu’à sa mort plus de 50 ans plus tard. Wallis faisait partie d’un groupe intéressé par les sciences naturelles et expérimentales qui est devenu la Royal Society. Wallis est donc un membre fondateur de la Royal Society et l’un de ses premiers boursiers. Wallis a largement contribué aux origines du calcul et était le mathématicien anglais le plus influent avant Newton.
https://mathshistory.st-andrews.ac.uk/Biographies/Wallis/
https://www.britannica.com/biography/John-Wallis