La révolution en Math : Géométries euclidiennes et non euclidiennes
Nikolaï Ivanovitch Lobatchevski (1792-1856)
Nikolaï Ivanovitch Lobatchevski (1792-1856) est un mathématicien russe du XIXe siècle, créateur d’une géométrie non-euclidienne. Il est né à Nizhny Novgorod dans une famille modeste. Son père décède alors qu’il est encore enfant, et sa mère décide alors de s’installer avec ses trois fils à Kazan, à 700 km environ à l’est de Moscou. Grâce à une bourse d’état, Lobachevsky peut étudier au lycée de Kazan de 1802 à 1807, puis à l’Université nouvellement créée (1804) de Kazan.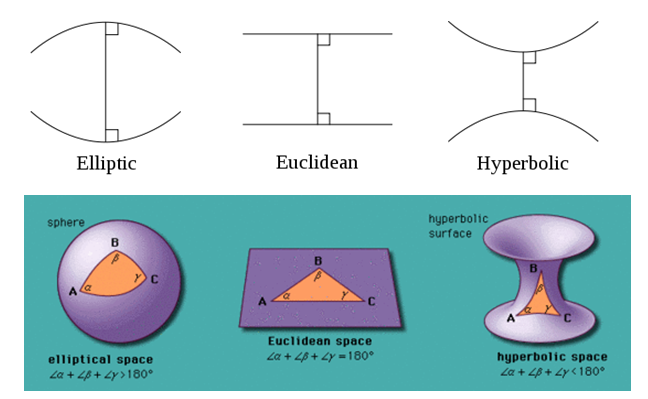 
A l’Université Nikolai Lobachevsky commence à s’engager dans des études de médecine. Il a des résultats excellents dans toutes les disciplines scientifiques. Mais il conteste plusieurs fois l’autorité des responsables de l’université et est même menacé d’être renvoyé. Il est sauvé de cela grâce à la protection de Bartels, son professeur de mathématiques, un ami de Gauss, qui a repéré ses capacités et le prend sous sa coupe. Lobachevsky est diplômé en 1811 et commence à enseigner à l’Université de Kazan en 1812. 
Il ne quittera pas cette université pendant 34 ans, occupant des postes de plus en plus élevés. Il en est même le recteur pendant 19 ans, de 1827 à 1846. Sous son mandat, et grâce aussi à la politique du tsar Nicolas I qui est beaucoup plus tolérante que celle de son prédécesseur Alexandre I, l’Université de Kazan est florissante : de nouveaux bâtiments sont construits, un observatoire est installé, le niveau scientifique et le nombre d’étudiants augmentent.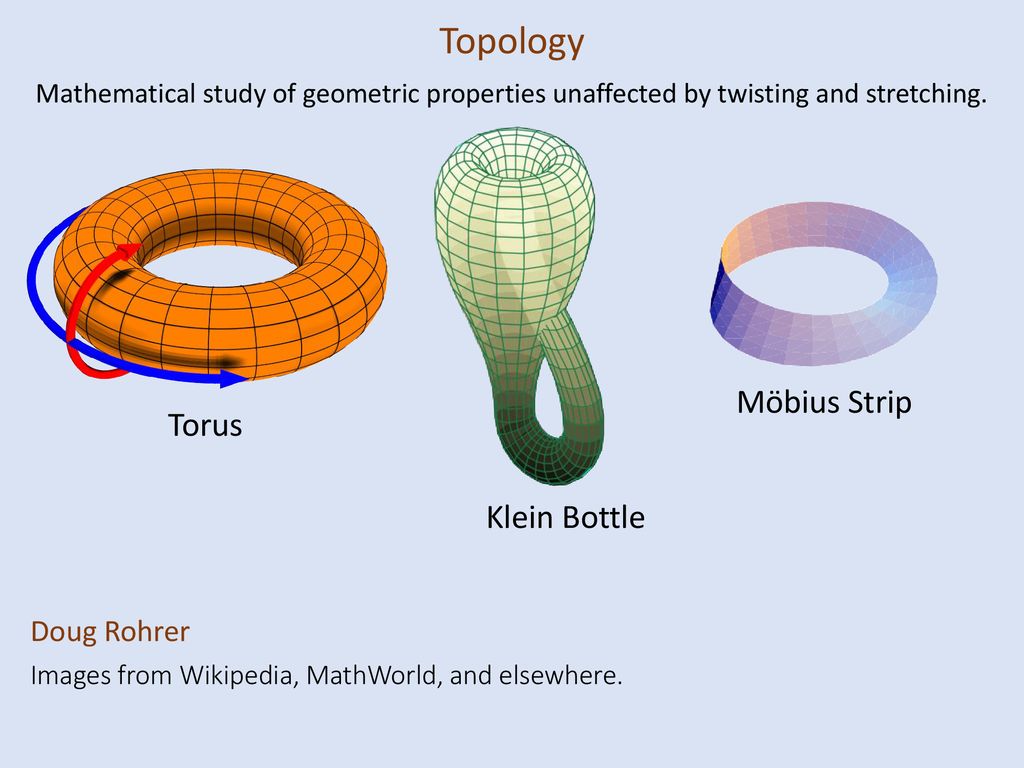
L’œuvre mathématique de Lobachevsky est centrée autour de la géométrie. Comme beaucoup d’autres avant lui, il commence par essayer de démontrer le 5ème axiome d’Euclide (étant donné un point et une droite ne passant pas par ce point, il existe une seule droite passant par ce point et parallèle à la première). Peu à peu germe en lui l’idée qu’il peut exister une autre géométrie, où on remplace cet axiome par un axiome très différent : par un point extérieur à une droite passe plus d’une droite parallèle à cette droite. Il expose pour la première fois cette idée dans un article de 1829, et continue de la développer jusqu’à son article Géométrie imaginaire de 1837. 
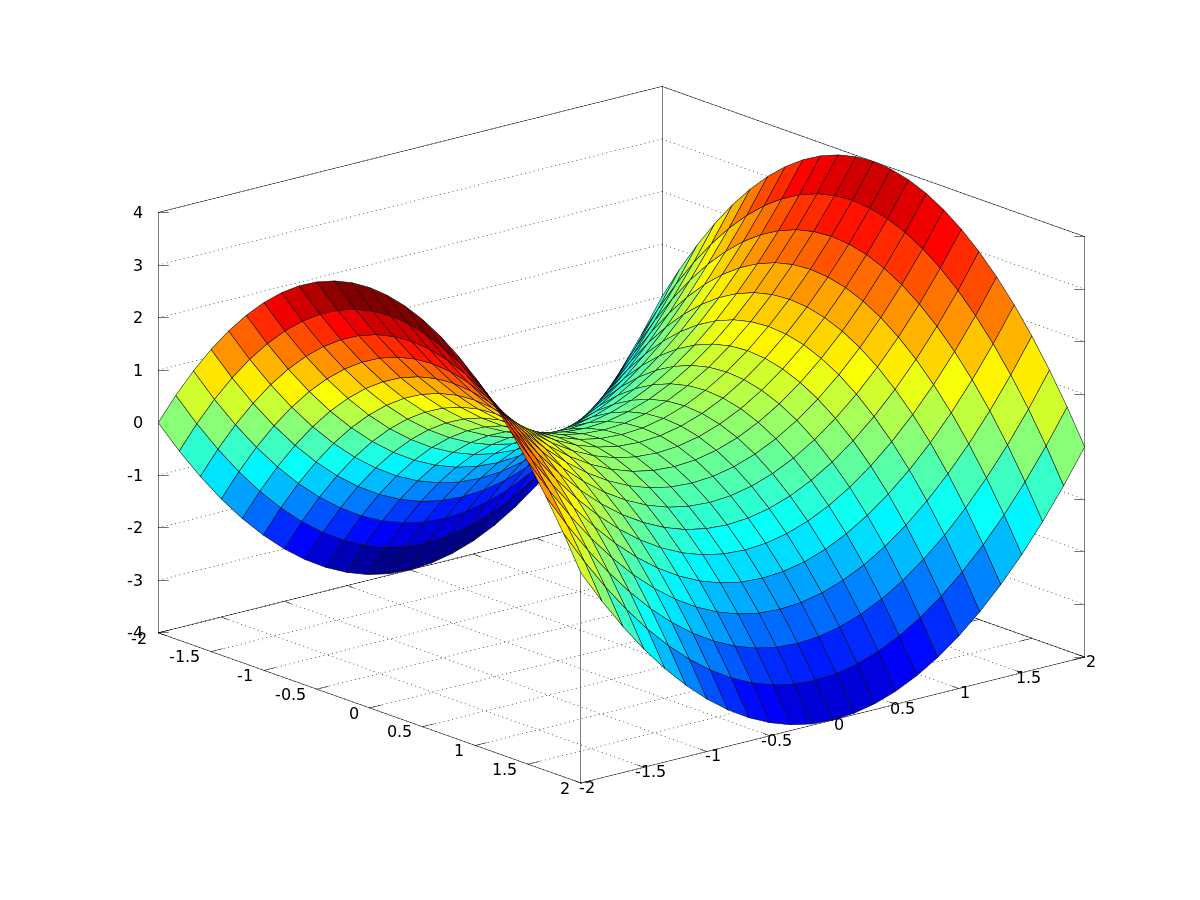Cette idée d’une géométrie non euclidienne est révolutionnaire, très en avance sur son temps, et elle est mal perçue par ses contemporains. Ainsi, Ostrogradsky refuse la publication de son article de 1829 au Saint Pétersbourg Math Journal. Gauss, ayant eu connaissance de ses travaux, dit pourtant en privé qu’ils sont très bons, mais ayant eu lui-même cette idée quelques années auparavant et ne l’ayant pas publiée, il n’en fait pas la propagande. Ainsi, les travaux de Lobachevsky sont restés très sous-estimés de son vivant. Vers la fin de sa vie, Lobachevsky devient aveugle. Il continue cependant de travailler et dicte son dernier ouvrage, Pangéométrie, où il fait un bilan de ses découvertes, à ses élèves.
Résumé de la géométrie non-euclidienne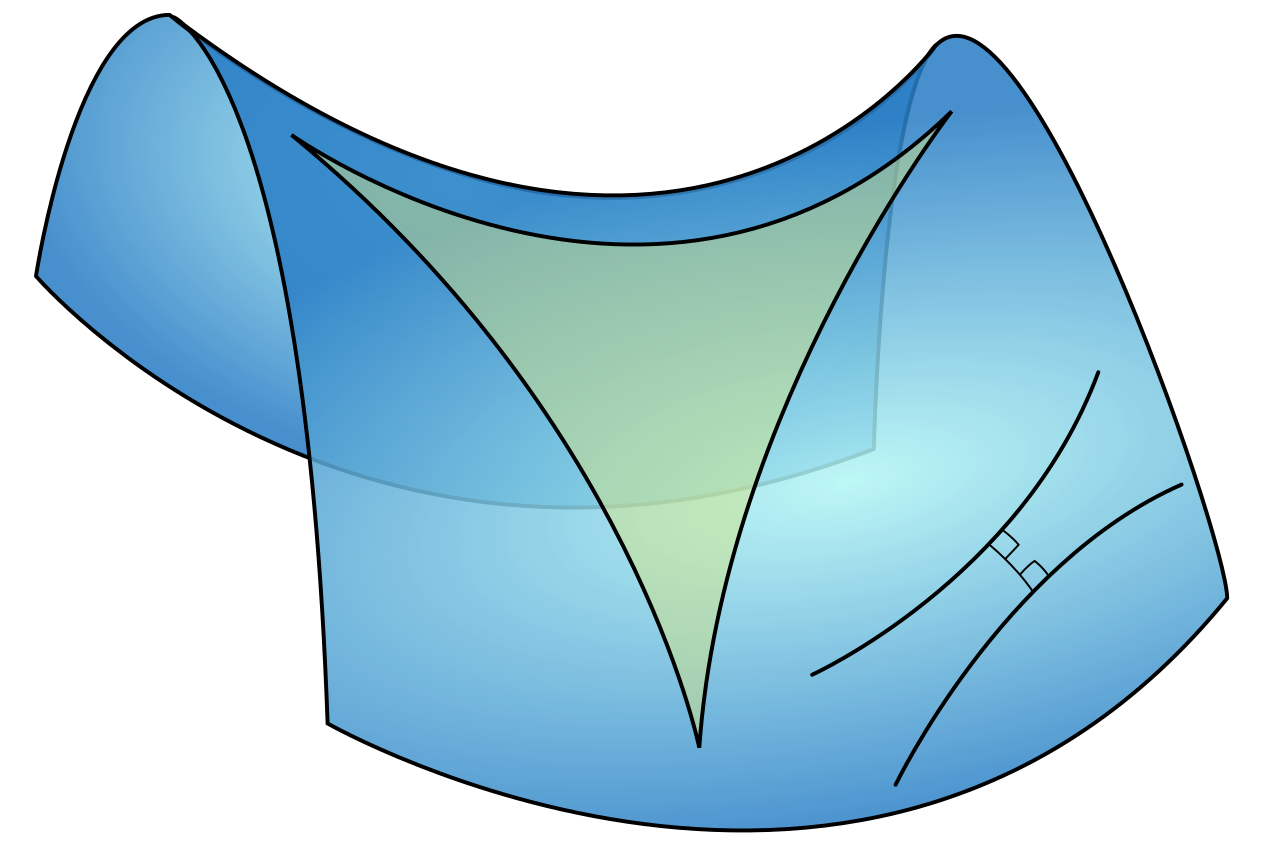
La géométrie a un rapport avec nos sensations et la bonne vieille géométrie d’Euclide n’est pas la seule possible, ni la seule utile. Le but de cet article est d’abord d’illustrer, sans aucune technicité, sur l’exemple de la géométrie élémentaire, les notions de théorie axiomatique, de déduction formelle, d’interprétation, d’indécidabilité (on montrera, à propos du postulat des parallèles, comment on peut parfois prouver tout naturellement qu’une proposition est indécidable dans une théorie donnée). On verra aussi que la géométrie a un rapport avec nos sensations et que la bonne vieille géométrie d’Euclide n’est pas la seule possible, ni la seule utile. On évoquera un monde non euclidien imaginé par Poincaré, et on conclura par un mot sur notre monde physique.
La géométrie d’Euclide
La géométrie euclidienne au sens des Éléments traite du plan et de l’espace ; elle est souvent présentée comme une géométrie « de la règle et du compas ». Les objets considérés sont les points, les segments, les droites, les demi-droites, avec leurs propriétés d’incidence (la règle), ainsi que les cercles (le compas).
Le livre 1 des Éléments de géométrie d’Euclide (vers l’an −300) commence par donner des « Définitions » des termes de la géométrie : « points », « lignes », « (lignes) droites », « angles », « cercles »,…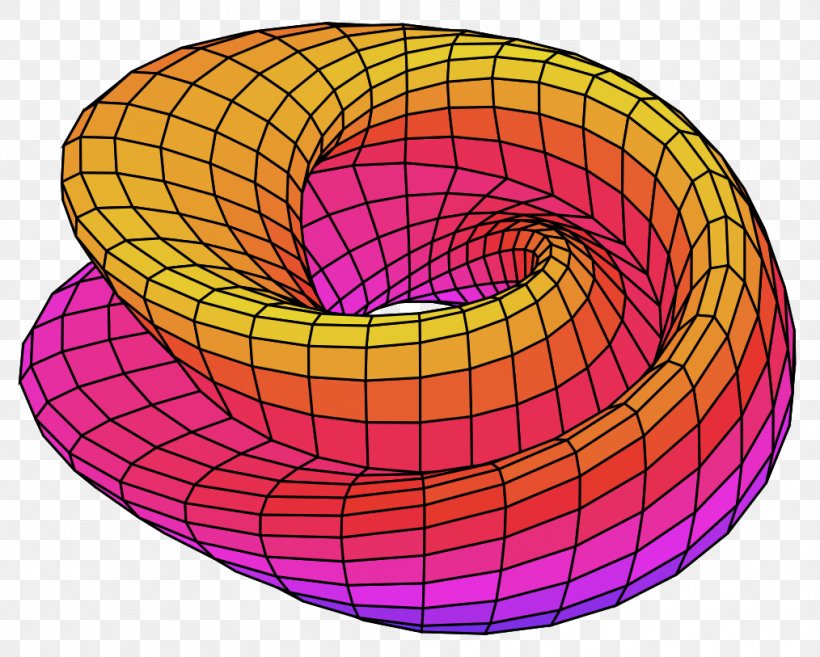
Une géométrie non euclidienne : la géométrie hyperbolique
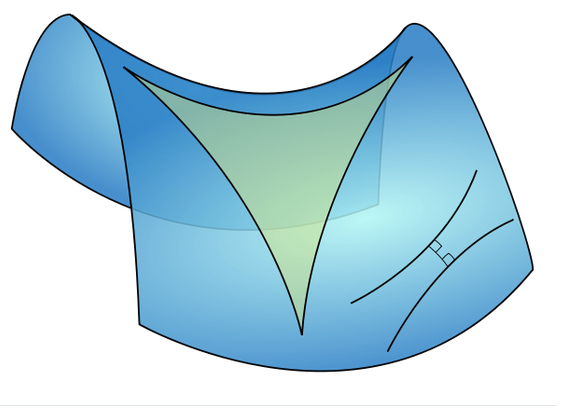
En mathématiques, on appelle géométrie non euclidienne une théorie géométrique ayant recours à tous les axiomes et postulats posés par Euclide dans les Éléments, sauf le postulat des parallèles.
Dans les années 1820-1830, Gauss, Lobatchevski et Bolyai se proposent (indépendamment) d’adjoindre à la géométrie absolue, non plus le postulat des parallèles, mais sa négation. En fait, ils lui adjoignent ce postulat : par un point extérieur à une droite donnée, il passe une infinité de parallèles à cette droite. 
Nikolaï Ivanovitch Lobatchevski (1792-1856)
Le père de Nikolai Ivanovich Lobachevsky, Ivan Maksimovich Lobachevsky, travaillait comme commis dans un bureau impliqué dans l’arpentage tandis que la mère de Nikolai Ivanovich était Praskovia Alexandrovna Lobachevskaya. Nikolai Ivanovich était l’un des trois fils de cette famille pauvre. Lorsque Nikolaï Ivanovitch avait sept ans, son père mourut et, en 1800 , sa mère déménagea avec ses trois fils dans la ville de Kazan, dans l’ouest de la Russie, aux confins de la Sibérie. 
Là, les garçons ont fréquenté le gymnase de Kazan , financé par des bourses du gouvernement, avec Nikolai Ivanovich entrant à l’école en 1802 . En 1807Lobachevsky est diplômé du Gymnasium et est entré à l’Université de Kazan en tant qu’étudiant libre. L’Université d’État de Kazan a été fondée en 1804 , résultat de l’une des nombreuses réformes de l’empereur Alexandre Ier, et elle a ouvert l’année suivante, deux ans seulement avant que Lobachevsky ne commence sa carrière de premier cycle. Son intention initiale était d’étudier la médecine, mais il a changé pour suivre un large cursus scientifique impliquant les mathématiques et la physique. 
Nikolai Lobatchevsky – Le Copernic de la géométrie
Le 24 février 1856 , le mathématicien et géomètre russe Nikolaï Ivanovitch Lobatchevski décède. Il est surtout connu pour ses travaux sur la géométrie hyperbolique . La principale réalisation de Lobachevsky est le développement (indépendamment de János Bolyai ) d’une géométrie non euclidienne , également appelée géométrie lobachevskienne .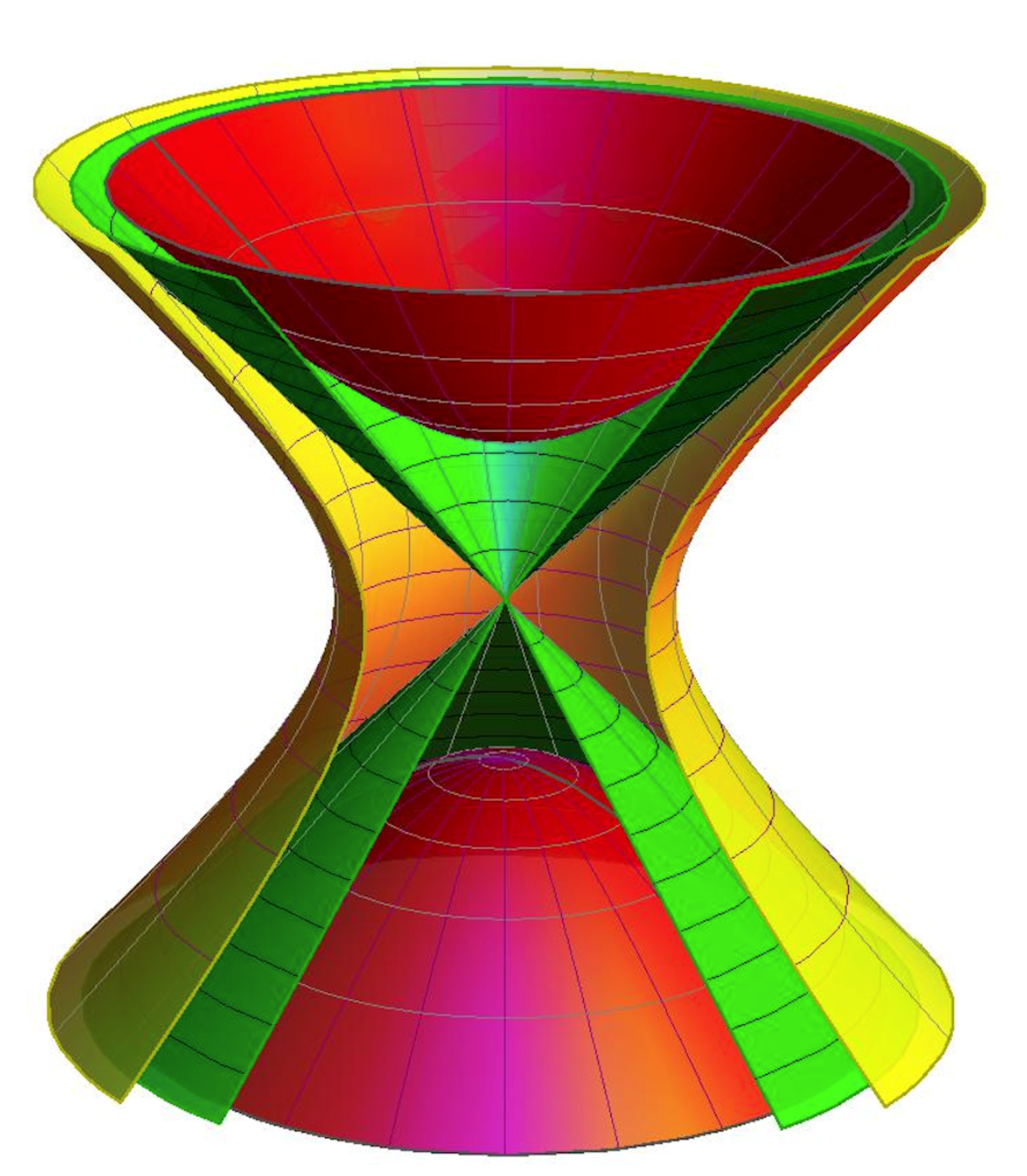
Nikolai Lobatchevsky – Petite enfance
Nikolai Lobachevsky est né comme l’un des trois enfants dans ou près de la ville de Nizhny Novgorod en Russie en 1792 de parents d’ origine polonaise . Son père Ivan Maksimovich Lobachevsky, commis dans un bureau d’ arpentage , est décédé à l’âge de sept ans et sa mère a déménagé à Kazan . Financé par des bourses du gouvernement , Lobachevsky a fréquenté le gymnase de Kazan à partir de 1802 , a obtenu son diplôme en 1807 et a ensuite reçu un bourse à l’ Université de Kazan , fondée trois ans plus tôt en 1804 . Son intention initiale était d’étudier la médecine, mais il a changé pour suivre un large cursus scientifique impliquant les mathématiques et la physique .
Carrière académique
À l’Université de Kazan , Lobachevsky a été influencé par le professeur Johann Christian Martin Bartels , un ancien professeur d’école et ami du mathématicien allemand Carl Friedrich Gauss . Bartels a été noté pour sa connaissance encyclopédique des mathématiques et a rapidement intéressé Lobachevsky aux mathématiques . Lobachevsky a obtenu une maîtrise en physique et en mathématiques en 1811 . En 1814 , il devient chargé de cours à l’Université de Kazan , en 1816, il est promu professeur associé , et en 1822 , à l’âge de 30 ans, il devient professeur titulaire , enseignant les mathématiques , la physique et l’astronomie, la même année où il a commencé une carrière administrative en tant que membre du comité formé pour superviser la construction de nouveaux bâtiments universitaires .Dernières années
En 1837Lobachevsky publie son article Géométrie imaginaire et un résumé de sa nouvelle géométrie Geometrische Untersuchungen zur Theorie der Parellellinien est publié à Berlin en 1840 . Cette dernière publication a beaucoup impressionné Gauss mais beaucoup a été écrit sur le rôle de Gauss dans la découverte de la géométrie non euclidienne, ce qui est tout simplement faux. Il y a une coïncidence qui découle du fait que nous savons que Gauss lui-même a découvert la géométrie non euclidienne mais l’a dit à très peu de gens, seulement ses amis les plus proches. Deux de ses amis étaient Farkas Bolyai , le père de János Bolyai (un découvreur indépendant de la géométrie non euclidienne ) et Bartels qui était le professeur de Lobachevsky. Cette coïncidence a suscité des spéculations selon lesquelles Lobachevsky et Bolyai ont été conduits à leurs découvertes par Gauss . M Kline a avancé cette théorie mais elle a été réfutée dans plusieurs travaux ; voir par exemple . Aussi Laptev dans a examiné la correspondance entre Bartels et Gauss et a montré que Bartels ne connaissait pas les résultats de Gauss en géométrie non euclidienne.
Il y a d’autres affirmations faites à propos de Lobachevsky et de la découverte de la géométrie non euclidienne qui ont été récemment réfutées. Par exemple dans les affirmations selon lesquelles Lobachevsky était en correspondance avec Gauss ( Gauss appréciait beaucoup les œuvres de Lobachevsky mais n’avait aucune correspondance personnelle avec lui ) , que Gauss étudiait le russe pour lire les articles russes de Lobachevsky comme le prétendait par exemple dans ( en fait , Gauss avait étudié le russe avant même d’avoir entendu parler de Lobachevsky ) , et que Gauss était un « bon propagandiste » des œuvres de Lobachevsky en Allemagne ( Gauss n’a jamais commenté publiquement l’œuvre de Lobachevsky ) se sont avérées fausses. 
L’histoire de l’acceptation de la géométrie hyperbolique de Lobachevsky est complexe et cette biographie n’est pas le lieu d’entrer dans les détails, mais nous en retiendrons les principaux événements. En 1866 , dix ans après la mort de Lobachevsky, Hoüel publie une traduction française des Geometrische Untersuchungen de Lobachevsky ainsi qu’une partie de la correspondance de Gauss sur la géométrie non euclidienne. Beltrami , en 1868, a donné une réalisation concrète de la géométrie de Lobachevsky. 
Weierstrass dirigea un séminaire sur la géométrie de Lobachevsky en 1870 auquel assista Klein et, deux ans plus tard, après que Klein et eurent discuté de ces nouvelles généralisations de la géométrie à Paris, Klein produisit sa vision générale de la géométrie comme les propriétés invariantes sous l’action de certains groupe de transformations dans le programme Erlanger . Il y avait deux autres contributions majeures à la géométrie de Lobachevsky par Poincaré en 1882 et 1887. Peut-être que ceux-ci marquent finalement l’acceptation des idées de Lobachevsky qui seraient finalement considérées comme des étapes vitales pour libérer la pensée des mathématiciens afin que la théorie de la relativité ait un fondement mathématique naturel.
Géométrie non euclidienne
La principale réalisation de Lobachevsky est le développement (indépendamment de János Bolyai ) d’une géométrie non euclidienne. Depuis la formulation axiomatique d’Euclide de la géométrie , les mathématiciens avaient essayé de prouver son cinquième postulat sous la forme d’un théorème déduit des quatre autres axiomes. Le cinquième postulat stipule que, étant donné une ligne et un point non sur la ligne , une ligne unique peut être tracée à travers le point parallèle à la ligne donnée . Lobatchevsky n’a pas essayé de prouver ce postulat en tant que théorème . Au lieu de cela, il a étudié la géométrie dans laquelle le cinquième postulat ne tient pas nécessairement. Lobachevsky a classé euclidien comme un cas particulier de cette géométrie plus générale . Cette idée a été rapportée pour la première fois en 1826 à la session du département de physique et de mathématiques , et la première publication de cette recherche est apparue en 1829 – 1830seulement dans un petit périodique de Kazan sous le titre Un aperçu concis des fondements de la géométrie , qui a été rejeté lorsqu’il a été soumis à l’ Académie des sciences de Saint-Pétersbourg pour publication .
Le postulat parallèle
Lobatchevsky a basé sa géométrie sur l’hypothèse suivante : dans le plan formé par une ligne et un point non sur la ligne, il est possible de tracer une infinité de lignes passant par le point qui sont parallèles à la ligne d’origine . Il a été prouvé plus tard que sa géométrie était auto-cohérente et, par conséquent , que le postulat parallèle est indépendant des autres axiomes d’ Euclide – par conséquent, ne peut pas en être dérivé en tant que théorème .
L’œuvre de Beltrami
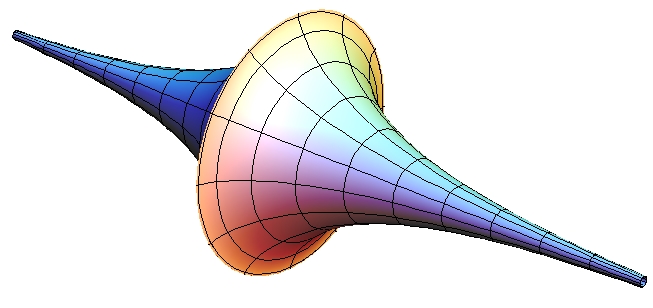
Lobachevsky a qualifié son travail de » géométrie imaginaire « , mais sympathisant de l’ esprit empirique de Francis Bacon , il a tenté de déterminer la « véritable » géométrie de l’espace en analysant les données astronomiques obtenues lors de la mesure de la parallaxe des étoiles . Une interprétation physique de la géométrie de Lobachevsky sur une surface de courbure négative a été découverte par le mathématicien italien Eugenio Beltrami en 1868 . Dans 1842 Le travail de Lobachevsky est remarqué et très apprécié par Gauss , à l’instigation duquel Lobachevsky est élu cette année -là membre correspondant de la Société royale de Göttingen .
Autres réalisations
En plus de sa géométrie , Lobachevsky a obtenu des résultats intéressants en algèbre et en analyse , comme le critère de Lobachevsky pour la convergence d’une série infinie ( 1834-1836 ). Ses intérêts de recherche comprenaient également la théorie des probabilités , le calcul intégral , la mécanique , l’ astronomie et la météorologie . La véritable signification de la nouvelle géométrie de Lobachevsky n’a été pleinement comprise et appréciée qu’avec les travaux de Bernhard Riemann sur les fondements de la géométrie ( 1868 ) et la preuve de la cohérence de la géométrie non euclidienne par Felix Klein en 1871.
Nikolaï Ivanovitch Lobatchevski (1792-1856)
Mathématicien russe qui, avec János Bolyai de Hongrie, est considéré comme le fondateur de la géométrie non euclidienne. Lobachevsky a construit et étudié un type de géométrie dans lequel le postulat parallèle d’Euclide est faux (le postulat stipule qu’à travers un point qui n’est pas sur une certaine ligne, une seule ligne peut être tracée sans rencontrer la première ligne). Cela n’a pas été bien accueilli au début, mais sa plus grande justification est venue avec l’avènement de la théorie de la relativité d’Einstein lorsqu’il a été démontré expérimentalement que la géométrie de l’espace n’est pas décrite par la géométrie d’Euclide. Outre la géométrie, Lobachevsky a également effectué des travaux importants sur la théorie des séries infinies, les équations algébriques, le calcul intégral et les probabilités.
https://culturemath.ens.fr/thematiques/superieur/geometries-euclidienne-et-non-euclidiennes
https://www.bibmath.net/bios/index.php?action=affiche&quoi=lobachevsky
https://mathshistory.st-andrews.ac.uk/Biographies/Lobachevsky/