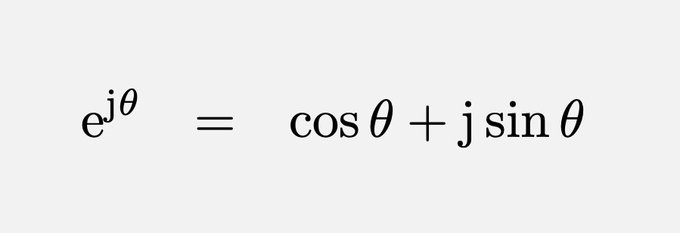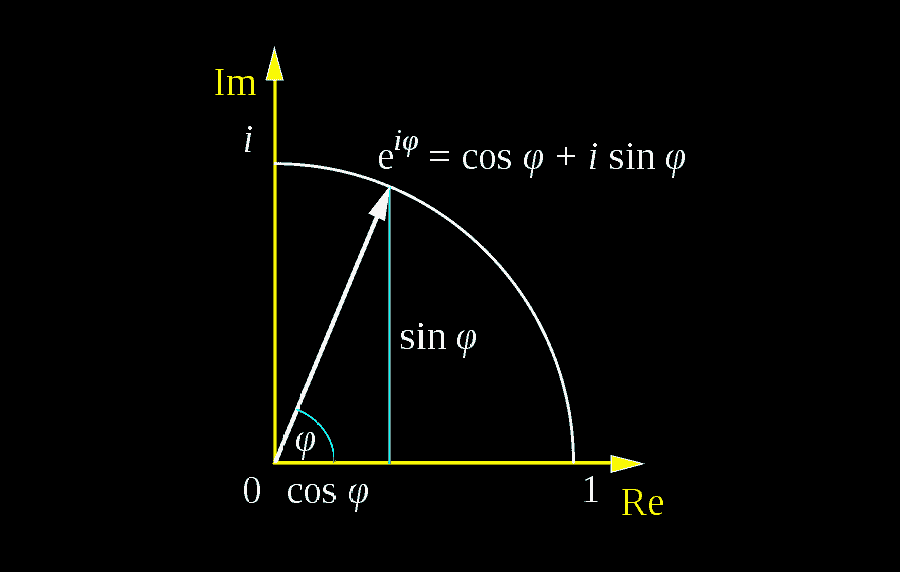Leonhard Euler (1707-1783) était un mathématicien suisse qui a apporté d’énormes contributions à un large éventail de mathématiques et de physique, notamment la géométrie analytique, la trigonométrie, la géométrie, le calcul et la théorie des nombres.
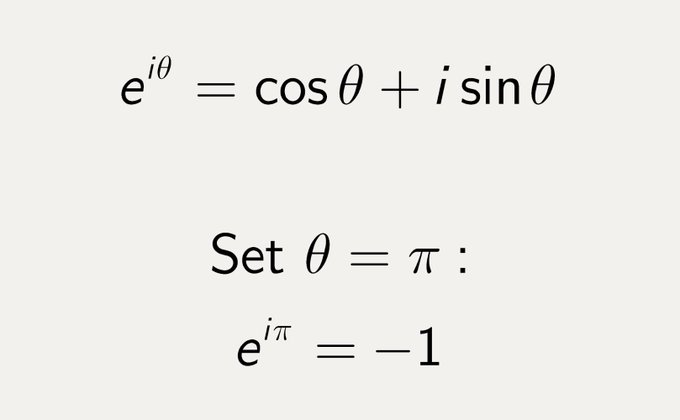
Leonhard Euler est né à Bâle, en Suisse, le 15 avril 1707. Fils de Paul Euler, pasteur protestant, et de Margaret Brucker, il déménage avec sa famille à l’âge d’un an dans la ville de Riehen, où il passe une grande partie de son enfance. Euler a été éduqué par son père qui lui a enseigné les premiers concepts des mathématiques. À l’âge de sept ans, il commence à étudier avec un tuteur privé et à lire divers textes. En 1720, à l’âge de 13 ans, Leonhard Euler retourne à Bâle pour étudier et se préparer à la théologie à l’université locale. Suivant les souhaits de sa famille, Leonhard Euler s’inscrit à la faculté de théologie. Bien que très religieux, il n’était pas enthousiasmé par l’étude de la théologie et se consacrait à l’étude des mathématiques pendant son temps libre.
Avec les encouragements du mathématicien Johann Bernoulli, qui découvre son talent pour les mathématiques, Euler entre dans le cours de mathématiques avancé en 1726. Grâce à ses relations amicales avec les frères de Johann, Nikolaus et Daniel, Euler est invité par l’impératrice Catherine à devenir membre de l’Académie des sciences de Saint-Pétersbourg en 1727. En 1730, Leonhard Euler devient professeur de physique à l’Académie, et en 1733, il remplace Daniel Bernoulli comme professeur de mathématiques. En 1734, il a épousé la Suissesse Katharina Gsell et ensemble ils ont eu 13 enfants, mais seuls cinq ont survécu. À cette époque, Euler publie plusieurs textes, dont le livre « Mécanique », dans lequel il présente de manière extensive la dynamique newtonienne sous forme d’analyse mathématique.
Enseignement
En 1741, le roi Frédéric II de Prusse l’invite à enseigner à Berlin. Euler devient alors titulaire de la chaire de mathématiques à l’Académie de Berlin, où il reste pendant 25 ans. En 1744, il est nommé directeur de la section mathématique de l’Académie.
À cette époque, il donne des leçons de physique à la princesse d’Anhalt-Dessau, nièce du roi, leçons qu’il publiera plus tard dans les célèbres Lettres à une princesse d’Allemagne (1772). Aveugle de l’œil droit à la suite d’une congestion cérébrale en 1735, Euler est ensuite complètement aveuglé par une opération de cataracte à l’œil gauche. Ce malheur ne le décourage pas et il poursuit son travail avec l’aide de son fils aîné.
Les réalisations d’Euler 
Il propose le célèbre pour le nombre Pi, la lettre i pour la racine carrée de -1 et le fameux e base des logarithmes népériens. Il établit à ce sujet, une formule liant ces trois nombres : e**iπ + 1 = 0 et une seconde mettant en relation la trigonométrie et l’analyse complexe : ei**x = cos x + i.sin x.
Leonhard Euler s’est penché sur presque toutes les branches des mathématiques. Parmi ses contributions les plus connues, citons l’introduction de la fonction gamma, l’analogie entre le calcul infinitésimal et le calcul des différences finies. Il a été le premier mathématicien à travailler avec les fonctions sinus et cosinus. En 1760, il se lance dans l’étude des lignes de courbure et commence à développer une nouvelle branche des mathématiques appelée géométrie différentielle. L’une de ses plus grandes réalisations a été le développement de la méthode des algorithmes avec laquelle il est parvenu, par exemple, à prédire les phases de la lune, afin d’obtenir des informations pour la préparation de tableaux destinés à aider le système de navigation.
Pendant son séjour à Berlin, Euler a écrit plus de 200 articles sur la physique, les mathématiques et l’astronomie et trois livres sur l’analyse mathématique. À la mort d’Euler, toujours en pleine activité, sa renommée s’est étendue à toute l’Europe. Euler est considéré comme le maître mathématicien du 18e siècle. Leonhard Euler est mort à Saint-Pétersbourg, en Russie, le 18 septembre 1783.
Leonhard Euler … Œuvres principales. 
Euler est l’auteur de trois grands traités sur l’analyse infinitésimale, dans lesquels il a exposé sa conception nouvelle du calcul différentiel et intégral et ses rapports avec la géométrie : l’Introductio in analysin infinitorum (1748), lesInstitutiones calculi differentialis (1755) et les Institutiones calculi integralis (3 vol., 1768-1770). Le premier livre de l’Introductio est consacré au calcul « algébrique » sur les fonctions, au second livre, il applique les méthodes et les résultats du premier livre à des problèmes de géométrie (étude des courbes algébriques ou transcendantes, surfaces, changements d’axes de coordonnées).
De fractionibus continuis (1737)
Introductio in analysis infinitorum (1748)
Institutiones calculi differentialis (1755)
Institutiones calculi integralis (1768-1770)
Vollständige Einleitung zur Algebra (1770)
Euler devient aveugle en 1771 mais continue à dicter ses textes scientifiques à ses fils ou à son valet grâce à sa mémoire colossale – il peut réciter 9 000 vers de l’Enéide par cœur. On raconte que se préparant à sa cécité inéluctable, il s’était progressivement habitué à ne plus écrire mais à dicter ses démonstrations. Il publie presque la moitié de son œuvre pendant ces 17 années de cécité, et certaines ont un succès colossal. L' » Introduction à l’algèbre » par exemple est un modèle de clarté et de rigueur que certain attribue à son handicap. Il meurt à 76 ans au cours d’une réunion avec des amis (il buvait du thé).
L’un des mathématiciens les plus importants du XVIIIe siècle et l’un des plus grands de l’histoire. Euler est largement considéré comme le mathématicien le plus prolifique de tous les temps, ses œuvres complètes remplissant 60 à 80 volumes in-quarto, plus que quiconque dans le domaine. Il a fait des découvertes importantes et influentes dans de nombreuses branches des mathématiques comme le calcul infinitésimal et la théorie des graphes et des contributions pionnières à la topologie et à la théorie analytique des nombres. 
Leonhard Paul Euler était un mathématicien et physicien suisse, l’un des fondateurs des mathématiques pures. Il a non seulement apporté des contributions décisives et formatrices aux sujets de la géométrie, du calcul, de la mécanique et de la théorie des nombres, mais a également développé des méthodes pour résoudre des problèmes d’astronomie d’observation et a démontré des applications utiles des mathématiques dans la technologie. À 28 ans, il s’est aveuglé un œil en fixant le soleil tout en travaillant à inventer une nouvelle façon de mesurer le temps.
Événements historiques
1741-06-19 Le mathématicien suisse Leonhard Euler quitte Saint-Pétersbourg pour un poste à l’Académie de Berlin, offert par Frédéric le Grand de Prusse
https://www.futura-sciences.com/sciences/personnalites/mathematiques-leonhard-euler-1812/
https://www.math93.com/index.php/histoire-des-maths/les-mathematiciens/200-euler-leonhard
https://www.maths-et-tiques.fr/index.php/histoire-des-maths/mathematiciens-celebres/euler
https://mathshistory.st-andrews.ac.uk/Biographies/Euler/