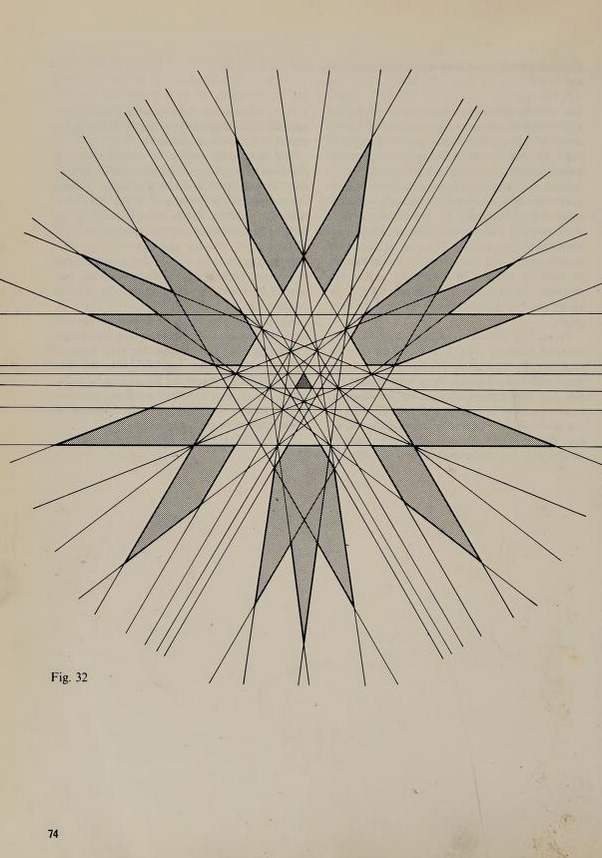
Magnus Wenninger était un mathématicien américain qui a construit des modèles de polyèdres et a écrit des livres à leur sujet.
Pr. Magnus Wenninger (1919-2017), BSF, I
Pr. Magnus Wenninger était un constructeur de modèles polyèdres incroyablement prolifique, ayant construit plusieurs milliers de modèles au cours de sa vie. Il est surtout connu pour son trio de livres de construction de modèles : Polyhedron Models, Spherical Models et Dual Models. Demandez à n’importe qui qui est un modéliste enthousiaste, et je parie qu’il en possède au moins un, sinon les trois.
Ces livres étaient importants car ils ouvraient le monde de la construction de modèles de polyèdres à un public beaucoup plus large, donnant des instructions détaillées sur la façon de construire des dizaines de modèles, ainsi que de discuter des mathématiques sous-jacentes aux polyèdres (bien que dans une mesure limitée).
Mais peut-être égal au P. Les capacités de construction de modèles de Wenninger étaient sa capacité à connecter les passionnés de polyèdres les uns avec les autres. Grâce à ses livres, d’autres maquettistes correspondaient avec lui en décrivant leurs intérêts particuliers, et il les mettait en relation avec d’autres qui lui avaient écrit avec des intérêts similaires. En 1996, il a créé une liste de diffusion où les personnes intéressées pouvaient échanger des idées sur tous les aspects des polyèdres. Il a été très actif pendant plusieurs années, mais du fait de la multiplication des sites sur les polyèdres ces dernières années, il l’est un peu moins aujourd’hui. Il est maintenant entretenu par le Dr Roman Mäder.
J’ai d’abord été présenté au P. Les livres de Wenninger en les trouvant parmi les piles de la bibliothèque de mathématiques et de sciences de Carnegie Mellon. Je ne me souviens pas combien de fois j’ai vérifié les modèles de polyèdres ; J’étais complètement absorbé. Je faisais des allers-retours, encore et encore, à la recherche de similitudes entre les différents modèles et les motifs géométriques sous-jacents.
J’ai commencé à correspondre avec Magnus à l’été 1993. J’ai toujours toute notre correspondance – je me suis assuré de photocopier toute lettre que je lui envoyais afin d’avoir un enregistrement continu de nos conversations polyédriques.
Malheureusement, Magnus Wenninger est décédé en février dernier à l’âge de 97 ans. Lorsque j’en ai entendu parler, j’ai pensé qu’il serait approprié d’organiser une session de communication invitée lors des Joint Mathematics Meetings (le 12 janvier 2018 à San Diego) en son honneur. J’ai invité certains de ses collègues de la liste de diffusion polyhedron, et d’autres aussi.
Ce matin, j’ai commencé à lire les lettres échangées avec Magnus en préparation d’une conférence que je donnerai à la session. Oui, c’était à l’époque où les gens écrivaient des lettres , et qui plus est, les écrivaient à la main. Incroyable! Un tel trésor intéressant d’idées et de pensées.
Pour mon discours, j’extrait le texte des lettres que Magnus m’a adressées, je prends des photos du texte et j’utilise ces extraits comme corps principal des diapositives. Je ne sais pas combien d’autres ont eu une longue correspondance avec Magnus, mais j’ai pensé que cela donnerait un aperçu unique de la vie de Magnus.
Et ainsi commence cette série de messages commémorant le P. Magnus Wenninger. Je vais continuer ce post en donnant un aperçu de notre relation. Puis plus tard, je partagerai avec vous quelques extraits de ses lettres, ainsi que des commentaires, le cas échéant. Il convient qu’on se souvienne de lui; l’organisation de la session d’articles invités en sa mémoire ainsi que l’écriture à son sujet dans mon blog seront ma contribution.
J’étais tout simplement fasciné par la beauté, la complexité – et dans une certaine mesure, la simplicité – des modèles polyèdres tridimensionnels. Mais j’étais aussi étudiant diplômé à Carnegie Mellon en mathématiques, ce qui n’était pas anodin.
Et quelle était la signification d’être un étudiant diplômé ? Eh bien, j’étais entraîné à penser rigoureusement, mathématiquement. À l’époque, cependant, tous les livres accessibles sur la géométrie polyédrique étaient à un niveau relativement élémentaire.
Ce que je veux dire, c’est ceci. Lorsque vous étudiez un polyèdre, de nombreuses caractéristiques métriques sont évidentes, telles que les longueurs d’arête et divers angles; par exemple, les angles entre deux faces d’un polyèdre (comme les angles à 90° entre les faces d’un cube). Et dans beaucoup de ces livres, ces longueurs et angles étaient donnés – mais dans la plupart des cas, uniquement dans des tableaux avec des approximations de suffisamment de chiffres significatifs nécessaires pour construire des modèles raisonnablement précis.
J’ai commencé à me demander comment tous ces chiffres étaient calculés. Je n’étais pas satisfait des résultats approximatifs ; Je voulais des résultats exacts . Ainsi commença mon autodidacte polyédrique, il y a une trentaine d’années.
Alors j’ai commencé à m’amuser, et quand j’ai terminé mes études supérieures, j’ai trouvé le courage d’écrire Magnus. J’étais plutôt intimidé à l’époque — je venais tout juste de commencer à apprendre les polyèdres, et il avait publié au moins trois livres sur le sujet ! Mais il s’avère que Magnus a été exceptionnellement généreux de son temps et de son talent, et a répondu en quelques semaines.
Ma lettre d’introduction était datée du 5 juillet 1993, et la dernière lettre que j’ai de Magnus porte la date du 22 octobre 1997. Je suis tout à fait sûr que c’est parce que nous avons continué notre correspondance en ligne. Cependant, la quasi-totalité de cette correspondance est perdue, car la majeure partie a été effectuée via une adresse e-mail universitaire à laquelle je n’ai plus accès.
Il y a quelques e-mails persistants dans mon compte gmail, depuis que ma correspondance avec Magnus a diminué après que j’ai quitté mon premier poste universitaire. Mais en plus d’entretenir une correspondance active avec Magnus, je lui ai rendu visite plusieurs fois à l’abbaye de St. John’s à Collegeville, MN. Je logerais dans une chambre d’amis à l’Abbaye et rejoindrais Magnus pour le déjeuner et le dîner. Tout au long de la journée, je visitais la chambre de Magnus où nous parlions de polyèdres, ou peut-être travaillais-je seul, ou simplement me promenais-je sur le campus.
Mes interactions avec Magnus étaient absolument inspirantes. En regardant les notes de ces années, je suis étonné de tout ce que j’ai accompli – et cela à une époque où l’infographie était beaucoup moins sophistiquée qu’elle ne l’est maintenant. Je partageais souvent les résultats avec Magnus dans mes lettres, et il fournissait sa perspective unique sur mon travail actuel. Même quand il était critique, il était toujours gentil.
Donc, dans mon prochain article, je commencerai à partager des extraits des lettres que Magnus m’a adressées. C’est, après tout, comment vous apprenez à connaître une personne – une interaction à la fois. J’espère que vous pourrez vous faire une idée de l’homme humble, brillant et généreux que Magnus était et continue d’être pour ceux qui l’ont bien connu. Son héritage se perpétue à travers nous, alors que nous nous efforçons d’être pour les autres ce que Magnus était pour nous.
En souvenir de Magnus Wenninger
Le père Wenninger était probablement le principal fabricant de modèles en papier de polyèdres dans le monde. Il y était depuis plus longtemps que n’importe qui d’autre ; son activité de modélisme a commencé à la fin des années 1950 dans le cadre de son approche de l’enseignement des mathématiques dans une école bénédictine des Bahamas. Déjà au milieu des années 60, il avait écrit un livret sur l’utilisation de modèles polyédriques en classe et, en 1971, il avait publié le livre « Polyhedron Models« , qui comprenait des photographies de modèles qu’il avait créés pour chacun des 75 polyèdres uniformes . Pour beaucoup de ces polyèdres, il s’agissait des premiers modèles physiques précis jamais créés.
Au cours de sa carrière, le père Wenninger a écrit deux autres livres sur les modèles mathématiques et de nombreux articles, comme celui-ci sur la couverture de la sphère avec des cercles.
Il a créé des modèles pour pratiquement tous ses écrits, et bien d’autres encore, dont beaucoup étaient des performances virtuoses dans l’art des constructions physiques d’objets géométriques, comme cette sculpture intitulée « Order in Chaos ».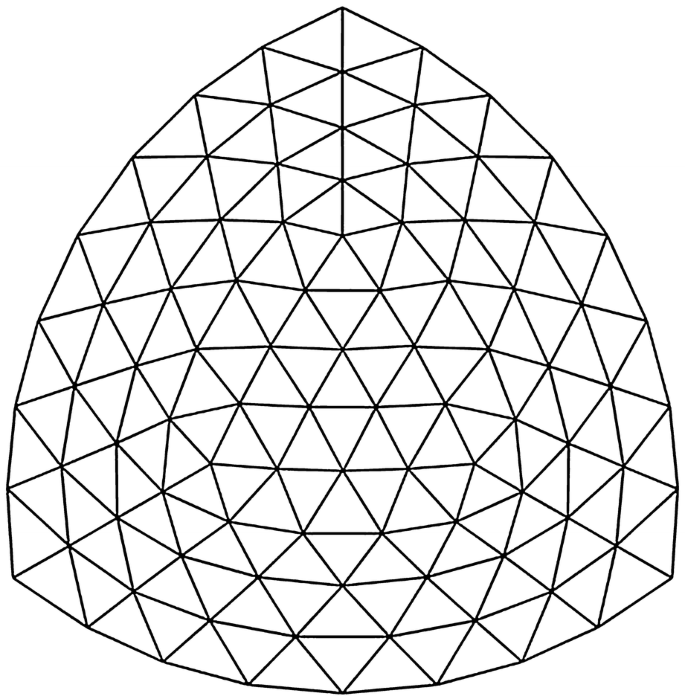
Que la vie et l’œuvre du Père Wenninger soient une source d’inspiration pour nous tous, mathématiciens. Nous terminons avec une sélection bien trop brève d’autres modèles montrant ses incroyables compétences et réalisations.
Biographie
Magnus Wenninger s’appelait Joseph Wenninger, prenant le nom monastique de Magnus après être devenu moine. Ses parents sont tous deux nés en Allemagne et ont émigré aux États-Unis, s’installant dans le Wisconsin. Magnus ( nous l’appellerons par ce nom bien qu’à l’époque il s’appelait Joe ) était le deuxième des sept enfants de ses parents. Son père était boulanger à Park Falls, une ville située à environ 70 km au sud de la rive sud du lac Supérieur. Magnus a fréquenté l’école primaire St Anthony à Park Falls de 1925 à 1933. Ses parents s’attendaient à ce que l’aîné de leurs garçons suive son père en devenant boulanger, et Magnus en tant que deuxième enfant à devenir prêtre. Lorsque Magnus avait environ treize ans, ses parents ont vu une publicité pour l’école préparatoire de Saint John, Collegeville, Minnesota, dans un journal allemand Der Wanderer . Les moines et prêtres de l’abbaye Saint-Jean, communauté bénédictine, avaient fondé l’école en 1857 . La raison de la connexion allemande était que les premiers bénédictins qui sont venus au Minnesota en 1856est originaire de l’abbaye bavaroise de Metten dans le sud-est de l’Allemagne. L’école préparait les garçons au collège bénédictin de l’Université St John, alors les parents de Magnus pensaient que ce serait le bon endroit pour que Magnus reçoive son éducation. Il entre à la Saint John’s Preparatory School en 1933 :-
J’avais le mal du pays d’être absent au début, mais à la fin de la première année, je m’étais fait tellement d’amis et j’aimais tellement ça que je ne suis jamais parti.
Après avoir obtenu son diplôme en 1937 , Wenninger entre à l’Université Saint John’s de Collegeville. Il a obtenu un baccalauréat en philosophie en 1942 , après avoir pris l’éducation comme matière mineure. Cependant, parallèlement à cela, il était entré à l’abbaye Saint-Jean et avait prononcé les vœux monastiques bénédictins le 11 juillet 1940 . Il fréquenta le Séminaire Saint John et fut ordonné prêtre catholique romain le 2 septembre 1945 . Lorsqu’il est entré dans l’Ordre de Saint-Benoît, on lui a donné le nom de Magnus, donc à partir de maintenant, nous l’appellerons le Père Magnus. À ce stade, l’éducation du père Magnus n’avait pas contenu beaucoup de mathématiques. Il a expliqué dans comment il a été conduit aux mathématiques:-
Après les cours habituels du secondaire, je n’ai eu qu’un semestre d’algèbre universitaire dans toutes mes études à St John’s. Un jour, après avoir été ordonné prêtre, l’Abbé m’a appelé pour me dire que l’Ordre ouvrait une école aux Bahamas, et il voulait que j’y aille et que j’y enseigne. « Qu’est-ce que je vais enseigner ? » J’ai demandé. « Ils te diront quand tu seras là-bas. » Mais il a dit qu’avant d’aller là-bas, je devrais aller à l’Université d’Ottawa et faire une maîtrise.
L’Abbé lui suggéra d’étudier la psychologie de l’éducation. Cependant :-
Quand je suis arrivé là-bas, j’ai constaté que presque tous les cours qui m’intéressaient étaient enseignés en français, ce que je n’avais jamais appris. Heureusement, il y avait un homme là-bas, Thomas Greenwood, du département de philosophie, qui était prêt à me donner un cours d’anglais, de logique symbolique. J’ai fait ma thèse de maîtrise sur ‘Le concept de nombre selon Roger Bacon et Albertus Magnus ‘. Il fallait que ce soit fait rapidement, car je devais me préparer pour descendre aux Bahamas.
Après avoir obtenu une maîtrise en philosophie de l’Université d’Ottawa en 1946, le père Magnus fut envoyé au St Augustine’s College, Nassau, aux Bahamas. Le directeur de l’école a dit qu’il avait besoin d’un professeur d’anglais et d’un professeur de mathématiques et a donné le choix au père Magnus. En raison des mathématiques qu’il avait étudiées pendant ses études de maîtrise, il a choisi les mathématiques qui, a-t-il dit, se sont avérées être la décision la plus importante de sa vie après avoir décidé de devenir moine bénédictin. Son enseignement n’était qu’au niveau élémentaire mais, après dix ans, il se sentait plutôt rassis et son directeur lui suggéra de suivre un cours d’été. Il a décidé de prendre une maîtrise au Columbia University Teachers College à New York en y étudiant pendant quatre sessions d’été. Il a obtenu sa maîtrise en enseignement des mathématiques en 1961 .
C’est pendant ses études au Columbia University Teachers College qu’il s’est intéressé aux polyèdres après avoir vu des modèles dans des vitrines le long des murs. Il a lu Mathematical Models de H Martyn Cundy et AP Rollett, puis The Fifty-nine Icosahedra de HSM Coxeter , P Du Val , HT Flather et JF Petrie. Après avoir lu ce livre, il a commencé à faire des modèles de tous les cinquante-neuf icosaèdres et de nombreux polyèdres uniformes. En 1966, le Conseil national des professeurs de mathématiques a publié les modèles de polyèdre du père Magnus pour la salle de classe. Le livret original contenait 40 pages mais l’édition révisée, publiée en 1975 , avait80 pages. Le père Magnus écrit dans l’introduction : –
Cette brochure, publiée pour la première fois en 1966 , a connu sa sixième impression en 1973 , constituant un total de 35 000 exemplaires imprimés. Ce seul fait atteste de l’intérêt continu pour ce travail de la part des enseignants et des étudiants.
Son résumé pour cette édition se lit comme suit : –
Cette deuxième édition explique le contexte historique et les techniques de construction de divers types de polyèdres. Sept feuilles à pli central sont incluses, contenant des dessins à grande échelle à partir desquels des filets ou des gabarits peuvent être fabriqués pour construire les modèles illustrés et décrits dans le texte. Des détails sont fournis pour la construction des cinq solides platoniques, des treize solides, stellations ou composés d’Archimède et d’autres polyèdres divers. Les modèles peuvent être utilisés pour illustrer les idées de symétrie, de réflexion, de rotation et de translation.
Après la publication de la première édition du livret en 1966 , le Père Magnus avait écrit à Donald Coxeter :-
Il a été très utile. Il m’a envoyé une copie de la monographie sur ‘Uniform Polyhedra’ écrite par lui-même, JCP Miller et MS Longuet-Higgins. C’était la première fois que je voyais une liste complète des soixante-quinze polyèdres uniformes. J’ai commencé à faire les modèles les uns après les autres, en utilisant du papier cartonné, du tagboard comme on l’appelait. J’en ai fait soixante-cinq, et ils étaient exposés dans ma classe. À ce moment-là, j’ai décidé de contacter un éditeur pour voir s’il serait intéressé par un livre. J’ai envoyé les photos et le texte à Cambridge University Press.
L’achèvement de la tâche de construction des dix polyèdres uniformes restants s’est avéré difficile et R Buckley de l’Université d’Oxford a aidé le père Magnus en fournissant les mesures précises. Le père Magnus a publié des modèles de polyèdre avec Cambridge University Press en 1971 . Donald Coxeter a écrit dans l’avant-propos du livre : –
Dans son style enthousiaste contagieux, l’auteur donne des instructions claires pour faire des modèles de nombreux types de polyèdres. Ces instructions sont illustrées par des photographies de sa propre collection, y compris ce qui est presque certainement le seul ensemble complet jamais réalisé à partir des polyèdres uniformes connus. Mais les photographies ne peuvent pas vraiment montrer les modèles dans toute leur splendeur. Les solides « snub » les plus compliqués sont non seulement extrêmement difficiles à fabriquer, mais aussi très décoratifs : un exemple parfait du lien entre la vérité et la beauté.
On pourrait être surpris par l’expression de Coxeter «polyèdres uniformes connus», mais il l’utilise avec précaution car au moment de la rédaction, on ne savait pas si les 75 polyèdres uniformes épuisaient la liste de ces polyèdres. Cependant, en 1975 , John Skilling de l’université de Cambridge prouva, à l’aide d’une recherche informatique, que la liste était complète.
Arthur Loeb écrit dans une revue des modèles Polyèdre :-
L’auteur décrit avec amour les pièges ou les effets spéciaux rencontrés avec chaque modèle, reflétant quinze années d’expérience dans l’assemblage de ces fascinantes et belles structures.
Le livre a également été révisé par DA Quadling qui écrit : –
… et c’est le livre à offrir à votre filleul préféré, ou peut-être à votre chef de service à l’occasion de son départ à la retraite ( car il y a là matière à passer 2000 happy hours ou plus ) .
Le père Magnus a enseigné les mathématiques au St Augustine’s College de Nassau jusqu’en 1971 , puis a passé les dix années suivantes en tant que comptable et contrôleur du Collège. En 1981, il est retourné au Minnesota et a passé trois ans comme comptable dans la presse liturgique, Ordre de Saint Benoît, Collegeville. Il a ensuite pris sa retraite mais a continué à vivre à l’abbaye Saint-Jean de Collegeville. 
Remarquablement, le père Magnus a publié plus de 25 livres et articles sur les mathématiques, principalement sur les polyèdres. Ses articles incluent Stellated Rhombic Dodecahedron Puzzle (1963) , The World of Polyhedrons (1965) , Some Facts About Uniform Polyedrons (1966) ,Fancy Shapes from Geometric Figures (1966) , Some Interesting Octahedral Compounds (1968) , A New Look for the Old Platonic Solids (1971) , ( with H Martyn Cundy ) A Compound of Five Dodecahedra (1976) , Geodesic Domes by Euclidean Construction ( 1978) , Avenues for Polyhedronal Research (1980) , Polyedrons and the Golden Number (1990) , et Artistic Tessellation Patterns on the Spherical Surface (1990) .
Pour terminer cette biographie, nous regardons deux autres livres publiés par le Père Magnus. Le premier d’entre eux estModèles sphériques (1979) , qui est décrit par E Jucovic dans une revue comme suit : –
Il s’agit du deuxième livre de l’auteur sur les modèles géométriques inspirés de HSM Coxeter et est écrit dans le même style que le premier [ Modèles polyèdres ] .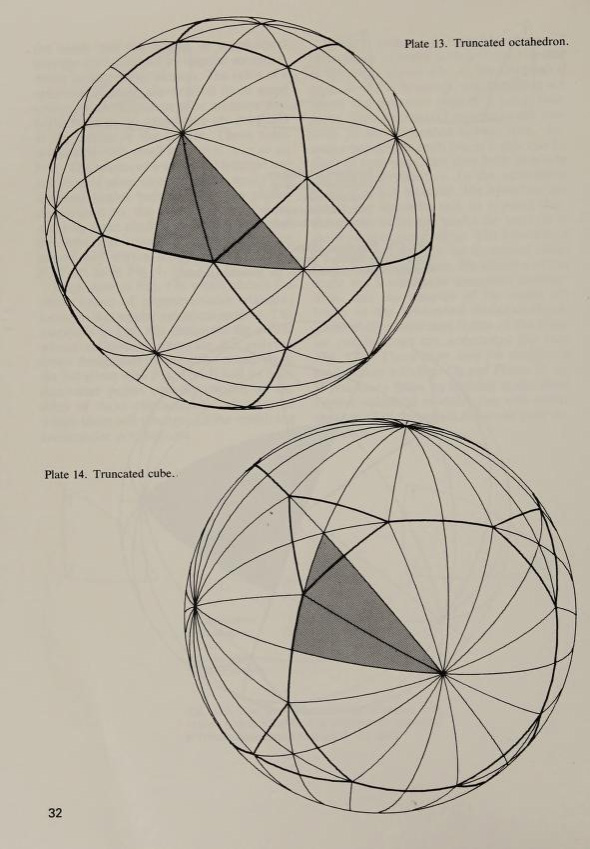 
Le livre a également été révisé par John Ede qui écrit : –
Cette suite des « Polyhedron Models » de l’auteur est tout ce à quoi s’attendent les passionnés du livre précédent ; admirablement clair, magnifiquement produit et vivant avec l’enthousiasme contagieux de Magnus Wenninger. Vous pouvez, comme le critique, avoir fait un grand nombre de modèles et peut même être synonyme de patience parmi vos amis et pourtant vous vous sentirez sûrement faible à l’idée de la collection de Wenninger. Ce livre est, cependant, plus que des instructions pour une série de modèles : les idées sous-jacentes sont expliquées avec suffisamment de détails pour ajouter grandement à sa satisfaction sans prendre le contrôle de ce qui est conçu comme un livre pratique.
Aussi David Brisson remarque que :-
… une étude aussi belle, claire et explicative de la classe des formes présentées par Wenninger est un délice.
Le deuxième des deux livres du père Magnus que nous allions examiner est Dual models (1983) . Il a été revu par Donald Coxeter :-
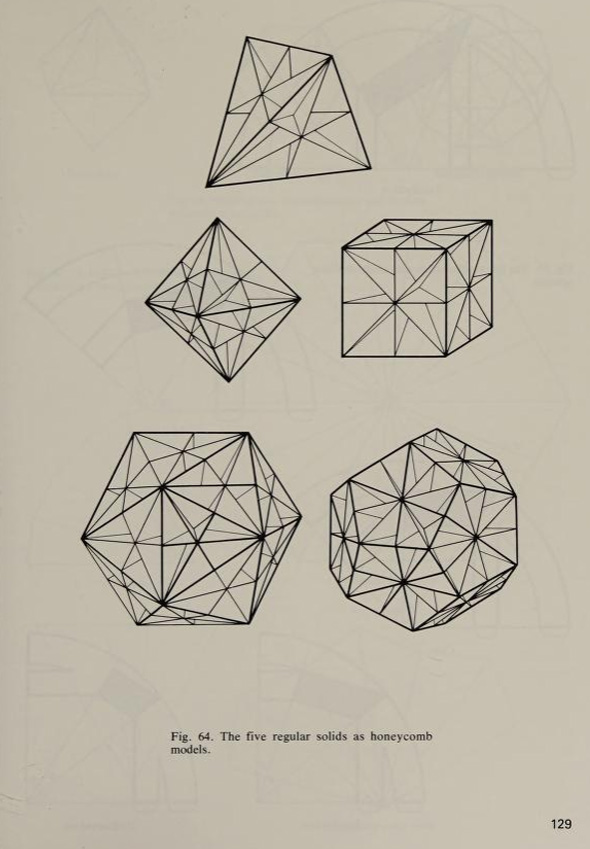
Enfin, nous citons la critique du livre de John Ede :-
Les maquettistes qui apprécient déjà les « modèles polyèdres » et les « modèles sphériques » accueilleront avec plaisir le nouveau livre de Wenninger. Encore une fois, c’est un volume qui est un plaisir à manipuler, avec des diagrammes clairs et de bonnes photographies, et qui fait honneur à l’éditeur ainsi qu’à l’auteur.
https://makezine.com/article/maker-news/math-monday-remembering-magnus-wenninger/
https://momath.org/mathmonday/remembering-magnus-wenninger/
https://mathshistory.st-andrews.ac.uk/Biographies/Wenninger/
https://cre8math.com/2018/01/01/fr-magnus-wenninger-o-s-b-i/