Thomas Bayes : redéfinir le probable
Thomas Bayes, mathématicien anglais
Thomas Bayes était un pasteur anglais qui a présenté sa théorie des probabilités en 1764 . Ses conclusions furent acceptées par Laplace en 1781 , redécouvertes par Condorcet, et restèrent incontestées jusqu’à ce que Boole les remette en cause. Depuis lors, les techniques de Bayes ont fait l’objet de controverses.
Thomas Bayes : biographie et contributions
Thomas bayes (1702-1761) était un théologien et mathématicien anglais, considéré comme le premier à avoir utilisé la probabilité inductive. De plus, il a développé un théorème qui porte son nom : le théorème de Bayes. Il a été le premier à établir une base mathématique pour l’inférence de probabilité : une méthode de calcul de la fréquence à laquelle un événement s’est produit précédemment et la probabilité qu’il se produise dans les tests futurs. On sait peu de choses sur le début et le développement de sa vie; cependant, on sait qu’il était membre de la Royal Society of London, une prestigieuse société scientifique du Royaume-Uni. D’autre part, le mathématicien anglais n’est pas arrivé à publier toutes ses oeuvres en vie; En fait, il n’a publié que deux ouvrages à petite échelle dont un seul était lié au domaine de la science et de manière anonyme.Après sa mort, ses travaux et notes ont été édités et publiés par le philosophe anglais Richard Price. Grâce à cela, on utilise aujourd’hui les travaux produits de leurs efforts.
Premières années et emplois : Thomas Bayes est né en 1701 ou 1702 ; la date exacte de sa naissance n’est pas connue. On dit qu’il est né à Londres ou dans le comté de Hertfordshire, en Angleterre. Il était le fils aîné des sept enfants de Joshua Bayes, un ministre presbytérien de Londres. Sa mère était Anne Carpenter. Bayes venait d’une famille protestante éminente qui ne se conformait pas aux règles de l’Église d’Angleterre, connue sous le nom de Mavericks. Ils ont été établis dans la ville anglaise de Sheffield. Pour cette raison, il a étudié avec des tuteurs privés et aurait reçu des cours d’Abraham de Moivre, un mathématicien français connu pour ses contributions à la théorie des probabilités, qui a eu une grande influence sur ses projets.
En raison de ses convictions religieuses radicales, il n’a pas pu s’inscrire dans des universités telles qu’Oxford ou Cambridge, il a donc étudié dans des écoles écossaises telles que l’Université d’Édimbourg. Il y étudie la logique et la théologie. En 1722, il rentre chez lui et aide son père à la chapelle avant de s’installer à Tunbridge Wells vers 1734. Il y reste, où il est ministre de la chapelle du Mont Sion, jusqu’en 1752.
Bienveillance divine : La bienveillance divine, ou une preuve intense que le but principal de la Divine Providence et du gouvernement est le bonheur de leurs christures, C’était l’un des premiers ouvrages publiés de Thomas Bayes, en l’an 1731. Bayes est connu pour n’avoir publié que deux ouvrages à petite échelle; l’un lié à la théologie et à la métaphysique et le second travail, lié au domaine scientifique plus orienté vers ce qu’étaient leurs apports. Le travail théologique métaphysique aurait été écrit en réponse à un mémoire du philosophe et ministre anglican John Balguy. 
Au cours des années précédentes, Balguy a publié un essai sur la Création et la Providence dans lequel il expliquait que le principe moral qui doit guider la vie humaine peut être les voies de Dieu ; c’est-à-dire que la bonté dans une divinité n’est pas une simple disposition à la bienveillance, mais un ordre et une harmonie. A partir de ce travail, Bayes a répondu avec sa publication et la controverse « si Dieu n’était pas obligé de créer l’univers, pourquoi l’a-t-il fait? »
Première publication scientifique : En 1736, une de ses premières publications scientifiques est publiée (anonymement), intitulée An introduction to the doctrine of Fluxions, and a defense of mathematicians against the objections of the author of The Analyst . Le travail consistait en une défense du calcul différentiel d’ Isaac Newton en réponse à l’attaque de l’évêque Berleley contre la théorie des fluxions et des séries infinies de Newton dans son ouvrage The Analyst , de 1730. Le travail de Bayes était essentiellement une défense des méthodes algébriques de Newton, dans lesquelles il permet de déterminer les maximums et les minimums des relations, des tangentes, des courbures, de l’aire et de la longueur. 
Cette publication a été celle qui a ouvert les portes à Thomas Bayes pour devenir membre de la Royal Society de Londres en 1742, bien qu’il n’ait pas publié d’ouvrages liés aux mathématiques. Malgré tout, son travail, initialement anonyme, a été découvert. Cela l’a amené à être invité à la Royal Society.
Motivations pour les mathématiques : Dans ses dernières années, il s’est intéressé aux théories des probabilités. L’historien de la statistique de Chicago, Stephen Stigler, pense que Bayes s’est intéressé au sujet après avoir examiné l’un des travaux du mathématicien anglais Thomas Simpson. Cependant, le statisticien britannique George Alfred Barnard pense qu’il a appris et a été motivé par les mathématiques après avoir lu un livre de son professeur Abraham Moivre.
Divers historiens pensent que Bayes était motivé pour réfuter l’argument de l’empiriste écossais David Hume incarné dans son travail. An Inquiry Concerning Human Understanding, dans laquelle il était contre les croyances miraculeuses. En plus des deux traités publiés, il a écrit plusieurs articles sur les mathématiques. L’un d’eux figurait dans une lettre adressée à John Canton, le secrétaire de la Royal Society of London. L’article a été publié en 1763 et traitait des séries divergentes et, plus précisément, des théorèmes de Moivre Stirling. Malgré cela, l’article n’a été commenté dans la correspondance d’aucun mathématicien de l’époque, il n’a donc apparemment pas eu une grande importance.
Mort et héritage : Bien qu’il n’y ait aucune preuve pour confirmer les activités de Bayes dans ses dernières années, on sait qu’il n’a jamais abandonné ses études en mathématiques; sinon, il est allé beaucoup plus loin dans la probabilité. D’autre part, Bayes ne s’est jamais marié, il est donc mort seul à Tunbridge Wells en 1761.
En 1763, on demanda à Richard Price d’être « l’exécuteur testamentaire littéraire » des œuvres de Thomas Bayes ; puis il a édité l’ouvrage intitulé Un essai pour résoudre un problème dans la doctrine des possibilités. Dans un tel travail est contenu le théorème de Bayes, l’un des résultats réussis des théories des probabilités. Plus tard, les travaux de Bayes sont restés ignorés au sein de la Royal Society de Londres et il a eu pratiquement peu d’influence sur les mathématiciens de l’époque.
Cependant, le marquis de Condorcet, Jean Antoine Nicolás Caritat, redécouvre les écrits de Thomas Bayes. Plus tard, le mathématicien français Pierre Simon Laplace les a prises en considération dans son ouvrage Théorie analytique des probabilités , en 1812. Aujourd’hui, son héritage se poursuit dans divers domaines des mathématiques.
Contributions Théorème de Bayes :
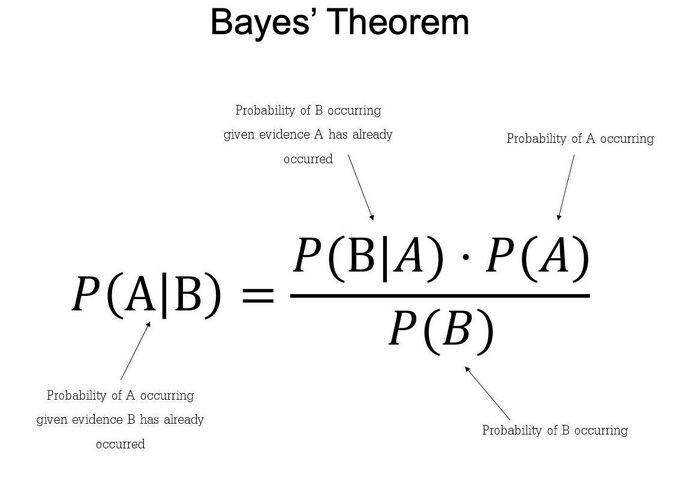
La solution de Bayes au problème de probabilité inverse (un terme obsolète pour la probabilité d’une variable non observée) a été présentée dans son ouvrage Un essai pour résoudre un problème dans la doctrine des possibilités, à travers son théorème. L’ouvrage fut lu par la Royal Society de Londres, en 1763, après sa mort.
Le théorème exprime la probabilité qu’un événement « A » se produise, sachant qu’il existe un événement « B » ; c’est-à-dire qu’il relie la probabilité de « A » compte tenu de « B » et de « B » compte tenu de « A ». Par exemple, la probabilité que vous ayez des douleurs musculaires étant donné que vous avez la grippe, vous pourriez connaître la probabilité d’avoir la grippe si vous avez des douleurs musculaires. Actuellement, le théorème de Bayes est appliqué en théorie des probabilités ; cependant, les statistiques d’aujourd’hui n’autorisent que des probabilités empiriquement fondées, et ce théorème n’offre que des probabilités subjectives. Malgré cela, le théorème permet d’expliquer comment toutes ces probabilités subjectives peuvent être modifiées. En revanche, elle peut s’appliquer à d’autres cas, tels que : les probabilités a priori ou a posteriori, dans le diagnostic du cancer, etc.
Bayésianisme : Le terme « bayésien » est utilisé depuis 1950 grâce aux progrès de la technologie informatique qui ont permis aux scientifiques de combiner les statistiques bayésiennes traditionnelles avec des techniques « aléatoires » ; l’utilisation du théorème s’est répandue dans la science et dans d’autres domaines.La probabilité bayésienne est une interprétation du concept de probabilité, qui permet de raisonner avec certaines hypothèses ; c’est-à-dire que les propositions peuvent être vraies ou fausses et le résultat sera complètement incertain.Les vues philosophiques de Bayes sur la probabilité sont difficiles à évaluer, puisque son essai n’aborde pas les questions d’interprétation. Cependant, Bayes définit la « probabilité » de manière subjective. Selon Stephen Stigler, Bayes a voulu ses résultats d’une manière plus limitée que les bayésiens modernes.Pourtant, les théories de Bayes étaient pertinentes pour développer, à partir de là, d’autres théories et règles actuelles. 
Inférence bayésienne : Thomas Bayes a donné lieu à son célèbre théorème pour expliquer d’autres événements. À l’heure actuelle, l’inférence bayésienne est appliquée à la théorie de la décision, à la vision par ordinateur (méthode de compréhension des images réelles afin de produire des informations numériques), etc. L’inférence bayésienne est un moyen de prédire plus précisément les données dont vous disposez actuellement ; En d’autres termes, c’est une méthode favorable lorsque vous n’avez pas assez de références et que vous souhaitez obtenir des résultats véridiques. Par exemple, il y a une probabilité assez élevée que le soleil se lève à nouveau le lendemain ; cependant, il y a une faible probabilité que le soleil ne se lève pas.L’interférence bayésienne utilise un stimulateur numérique pour confirmer le degré de croyance en l’hypothèse avant d’observer les preuves et, en même temps, calcule le nombre du degré de croyance en l’hypothèse après l’observation. L’interférence bayésienne est basée sur des degrés de croyances ou de probabilités subjectives.
Thomas Bayes : redéfinir le probable
Ce n’est pas souvent de nos jours que nous attribuons une percée majeure en sciences ou en mathématiques à quelqu’un qui a un diplôme en théologie. Cependant, bon nombre des percées scientifiques les plus importantes de l’histoire sont venues de théologiens et d’ecclésiastiques qui se sont aventurés dans le monde de la science à la recherche de connaissances qu’ils ne pouvaient pas obtenir des textes religieux.
Thomas Bayes, par exemple, était un ministre preysbytérien qui a passé la majeure partie de sa vie professionnelle consacrée aux questions de religion. Cependant, il nourrissait un intérêt pour la science et était ouvert à l’exploration d’idées et de théories que de nombreux membres de l’establishment religieux considéraient comme menaçantes .
« En science, le progrès est possible. En fait, si l’on croit au théorème de Bayes, le progrès scientifique est inévitable à mesure que des prédictions sont faites et que les croyances sont testées et affinées.
Prise en charge de l’établissement : Bayes a grandi dans une famille aisée du nord de l’Angleterre. Son père était ministre de l’Église presbytérienne, qui à l’époque était qualifiée de « non-conformiste » en raison de son mépris ouvert de la doctrine de l’Église d’Angleterre. Les non-conformistes ont subi divers niveaux de persécution au cours des XVIIe, XVIIIe et XIXe siècles, notamment l’interdiction d’exercer des fonctions publiques et de fréquenter des universités d’élite, telles qu’Oxford et Cambridge. 
Bayes a suivi les traces de son père dans le clergé et n’a pas hésité à la controverse. En 1731, il publia un tract largement diffusé affirmant que les actions de Dieu étaient motivées par la bienveillance et le « bonheur de ses créatures ». Cela peut sembler une affirmation bénigne maintenant, mais à l’époque, cela a suscité une attention considérable, ainsi que des réactions négatives de la part des autres membres du clergé. Cinq ans plus tard, Bayes publia un tract défendant la théorie du calcul d’Isaac Newton, que le philosophe irlandais George Berkeley avait récemment attaquée dans son propre tract.
Probabilité sans fin : Bayes n’a pas vécu assez longtemps pour voir sa contribution la plus importante à la science et aux mathématiques publiée. Un Essai vers la résolution d’un problème dans la Doctrine des Chances , qui comprenait ce que l’on appelle maintenant le Théorème de Bayes, a été publié en 1763, deux ans après la mort de Bayes.
Les arguments de Bayes offraient une nouvelle compréhension de la probabilité. Alors que le concept de probabilité avait déjà été utilisé par les mathématiciens, il n’était généralement utilisé que pour décrire une séquence observable d’événements. Bayes, cependant, a introduit une théorie du calcul des probabilités lorsque certaines variables sont inconnues. Bayes a donné l’exemple d’une personne regardant un jeu de loterie qui comprend un nombre inconnu de prix et de blancs. Si les 11 premiers tirages comprennent 10 blancs et un lot, le témoin peut en déduire que le ratio des blancs sur les lots est compris entre 9:1 et 11:1, mais avec un nombre inconnu de lots et de blancs restants, il y a des chances qu’il ait raison est inférieur à 8 %. Cependant, plus la taille de l’échantillon augmente, plus il est probable que le ratio observé reflète le ratio réel.
Le théorème de Bayes continue d’être une partie importante des statistiques et est utilisé dans une variété de domaines. Par exemple, il est utilisé dans les tests génétiques pour déterminer la probabilité qu’un patient développe une certaine maladie, comme le cancer. Il a également été utilisé pour développer des algorithmes, tels que ceux qui sont utilisés pour filtrer les spams en observant des modèles de texte.
Preuve de Dieu ? Le monde n’aurait peut-être jamais entendu parler du théorème de Bayes sans Richard Price, qui a découvert l’essai et l’a fait publier. Pour Price, un collègue ministre presbytérien, les implications du théorème s’étendaient bien au-delà des mathématiques. Les lois que Bayes a énoncées, a-t-il dit, étaient la preuve de l’existence de Dieu . Il expliqua: Le but que je veux dire est de montrer quelle raison nous avons de croire qu’il y a dans la constitution des choses des lois fixes selon lesquelles les événements se produisent, et que, par conséquent, le cadre du monde doit être l’effet de la sagesse et de la puissance d’un cause intelligente ; et ainsi de confirmer l’argument tiré des causes finales pour l’existence de la Divinité.
Bayes a été élu membre de la Royal Society en 1742 malgré le fait qu’à cette époque il n’avait aucun ouvrage publié sur les mathématiques, en effet aucun n’a été publié de son vivant sous son propre nom, l’article sur les fluxions mentionné ci-dessus a été publié de manière anonyme. Une autre publication mathématique sur les séries asymptotiques est apparue après sa mort où il a montré que la série pour enregistrer z ! donnée par Stirling et de Moivre , n’était pas valable puisqu’elle divergeait. 
Il y a quelques autres éléments de mathématiques qui nous sont parvenus de Bayes et nous en examinons maintenant quelques-uns. La première que nous mentionnons est une lettre qu’il a écrite, probablement vers 1756 . Bayes a écrit :- Vous vous souvenez peut-être que nous parlions il y a quelques jours de la tentative de M. Simpson de montrer le grand avantage de faire la moyenne entre plusieurs observations astronomiques plutôt que de se fier à une seule observation soigneusement faite, afin de diminuer les erreurs provenant de l’imperfection de instrument et les organes des sens.
En fait, Simpson avait fait la même erreur que les Français feraient près de cinquante ans plus tard avec le cercle répétitif de Borda , en croyant qu’on pouvait rendre l’erreur d’observation aussi petite qu’on le désirait en faisant des observations multiples. Cependant, Bayes s’est rendu compte que ce n’était pas le cas et a écrit dans sa lettre : –Or que les erreurs provenant de l’imperfection de l’instrument et des organes des sens soient ainsi réduites à néant ou à peu près rien qu’en multipliant le nombre des observations me paraît extrêmement invraisemblable. Au contraire, plus vous faites d’observations avec un instrument imparfait, plus il semble que l’erreur dans votre conclusion sera proportionnelle à l’imperfection de l’instrument utilisé…
Dans un cahier qui a été presque certainement écrit par Bayes est examiné en détail. Ce cahier contient une quantité considérable de travaux mathématiques, y compris des discussions sur les probabilités, la trigonométrie, la géométrie, la résolution d’équations, les séries et le calcul différentiel. Il y a aussi des sections sur la philosophie naturelle dans lesquelles Bayes aborde des sujets tels que l’électricité, l’optique et la mécanique céleste.Thomas Bayes (1702-1761) 
Théologien et mathématicien anglais qui a été le premier à utiliser la probabilité de manière inductive et qui a établi une base mathématique pour l’inférence de probabilité (un moyen de calculer, à partir de la fréquence avec laquelle un événement s’est produit lors d’essais antérieurs, la probabilité qu’il se produise lors d’essais futurs) . Cela est devenu la base d’une technique statistique, maintenant appelée estimation bayésienne, pour calculer la probabilité de la validité d’une proposition sur la base d’une estimation préalable de sa probabilité et de nouvelles preuves pertinentes. Les statisticiens ultérieurs citent les inconvénients de la méthode, notamment les différentes manières d’attribuer des distributions antérieures de paramètres et la sensibilité possible des conclusions au choix des distributions.:max_bytes(150000):strip_icc()/Bayes_Theorem-v2-6d6b2a2293c648ec99f16f78a3c80f09.png)
https://warbletoncouncil.org/thomas-bayes-7012
https://www.historyofdatascience.com/thomas-bayes/