Biographie de Gottfried Wilhelm Leibniz, philosophe et mathématicien
Gottfried Wilhelm Leibniz était un éminent philosophe et mathématicien allemand. Bien que Leibniz était un polymathe qui a contribué à de nombreux travaux dans de nombreux domaines différents, il est surtout connu pour ses contributions aux mathématiques, dans lesquelles il a inventé le calcul différentiel et intégral indépendamment de Sir Isaac Newton. En philosophie, Leibniz est connu pour ses contributions sur un large éventail de sujets, y compris «l’optimisme» – l’idée que le monde actuel est le meilleur de tous les mondes possibles, et a été créé par un Dieu pensant librement qui l’a choisi pour une bonne raison.
En bref : Gottfried Wilhelm Leibniz 
Naissance : 1er juillet 1646 à Leipzig, Allemagne
Décédé : 14 novembre 1716 à Hanovre, Allemagne
Parents : Friedrich Leibniz et Catharina Schmuck
Formation : Université de Leipzig, Université d’Altdorf, Université d’Iéna
Jeunesse et carrière
Gottfried Wilhelm Leibniz est né à Leipzig, en Allemagne, le 1er juillet 1646, de Friedrich Leibniz, professeur de philosophie morale, et de Catharina Schmuck, dont le père était professeur de droit. Bien que Leibniz ait fréquenté l’école primaire, il était surtout autodidacte à partir des livres de la bibliothèque de son père (décédé en 1652 alors que Leibniz avait six ans). Alors qu’il était jeune, Leibniz s’est plongé dans l’histoire, la poésie, les mathématiques et d’autres matières, acquérant des connaissances dans de nombreux domaines différents. En 1661, Leibniz, qui avait 14 ans, commença des études de droit à l’Université de Leipzig et fut exposé aux travaux de penseurs tels que René Descartes, Galilée et Francis Bacon. Là-bas, Leibniz a également fréquenté l’école d’été de l’Université d’Iéna, où il a étudié les mathématiques. En 1666, il termine ses études de droit et postule pour devenir doctorant en droit à Leipzig. En raison de son jeune âge, cependant, il s’est vu refuser le diplôme. Cela a poussé Leibniz à quitter l’Université de Leipzig et à obtenir le diplôme l’année suivante à l’Université d’Altdorf, dont les professeurs ont été tellement impressionnés par Leibniz qu’ils l’ont invité à devenir professeur malgré sa jeunesse. Leibniz, cependant, a refusé et a plutôt choisi de poursuivre une carrière dans la fonction publique.
Le mandat de Leibniz à Francfort et Mayence, 1667-1672 
En 1667, Leibniz entre au service de l’électeur de Mayence, qui le charge d’aider à réviser le Corpus Juris – ou corps de lois – de l’électorat. Pendant ce temps, Leibniz a également travaillé pour réconcilier les partis catholiques et protestants et a encouragé les pays européens chrétiens à travailler ensemble pour conquérir des terres non chrétiennes, au lieu de se faire la guerre. Par exemple, si la France laissait l’Allemagne seule, alors l’Allemagne pourrait aider la France à conquérir l’Égypte. L’action de Leibniz a été inspirée par le roi de France Louis XIV, qui s’est emparé de certaines villes allemandes d’Alsace-Lorraine en 1670. (Ce « plan égyptien » serait finalement transmis, bien que Napoléon ait involontairement utilisé un plan similaire plus d’un siècle plus tard.)
Paris, 1672-1676
En 1672, Leibniz se rendit à Paris pour discuter davantage de ces idées, y restant jusqu’en 1676. À Paris, il rencontra un certain nombre de mathématiciens comme Christiaan Huygens, qui fit de nombreuses découvertes en physique, en mathématiques, en astronomie et en horlogerie. L’intérêt de Leibniz pour les mathématiques a été attribué à cette période de voyage. Il a rapidement progressé dans le sujet, découvrant le cœur de certaines de ses idées sur le calcul, la physique et la philosophie. En effet, en 1675, Leibniz découvrit les fondements du calcul intégral et différentiel indépendamment de Sir Isaac Newton. En 1673, Leibniz a également fait un voyage diplomatique à Londres, où il a montré une machine à calculer qu’il avait développée appelée Stepped Reckoner, qui pouvait additionner, soustraire, multiplier et diviser. À Londres, il est également devenu membre de la Royal Society, un honneur décerné aux personnes qui ont apporté une contribution substantielle à la science ou aux mathématiques.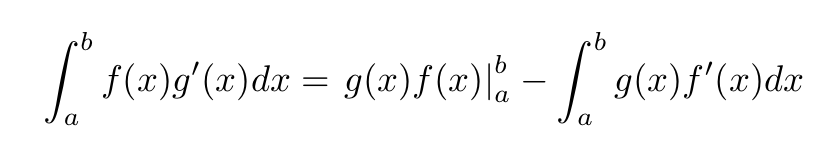
Hanovre, 1676-1716
En 1676, à la mort de l’électeur de Mayence, Leibniz s’installe à Hanovre, en Allemagne, et est chargé de la bibliothèque de l’électeur de Hanovre. C’est à Hanovre – l’endroit qui lui servira de résidence pour le reste de sa vie – que Leibniz portait de nombreux chapeaux. Par exemple, il a été ingénieur minier, conseiller et diplomate. En tant que diplomate, il a continué à faire pression pour la réconciliation des églises catholique et luthérienne en Allemagne en écrivant des articles qui résoudraient les points de vue des protestants et des catholiques. La dernière partie de la vie de Leibniz a été en proie à la controverse, la plus notable étant en 1708, lorsque Leibniz a été accusé d’avoir plagié le calcul de Newton alors qu’il avait développé les mathématiques de manière indépendante. Leibniz est mort à Hanovre le 14 novembre 1716. Il avait 70 ans. Leibniz ne s’est jamais marié et ses funérailles n’ont été suivies que par son secrétaire personnel.
Leibniz était considéré comme un grand polymathe et il a apporté de nombreuses contributions importantes à la philosophie, à la physique, au droit, à la politique, à la théologie, aux mathématiques, à la psychologie et à d’autres domaines. Il est peut-être plus connu, cependant, pour certaines de ses contributions aux mathématiques et à la philosophie. À la mort de Leibniz, il avait écrit entre 200 000 et 300 000 pages et plus de 15 000 lettres de correspondance à d’autres intellectuels et politiciens importants, dont de nombreux scientifiques et philosophes notables, deux empereurs allemands et le tsar Pierre le Grand.
Contributions aux mathématiques 
Système binaire moderne
Leibniz a inventé le système binaire moderne, qui utilise les symboles 0 et 1 pour représenter des nombres et des déclarations logiques. Le système binaire moderne fait partie intégrante du fonctionnement et de l’exploitation des ordinateurs, même si Leibniz a découvert ce système quelques siècles avant l’invention du premier ordinateur moderne. Il convient de noter, cependant, que Leibniz n’a pas lui-même découvert les nombres binaires. Les nombres binaires étaient déjà utilisés, par exemple, par les anciens Chinois, dont l’utilisation des nombres binaires était reconnue dans l’article de Leibniz qui introduisait son système binaire (« Explanation of Binary Arithmetic », publié en 1703).
Calcul
Leibniz a développé une théorie complète du calcul intégral et différentiel indépendamment de Newton, et a été le premier à publier sur le sujet (1684 contre 1693 de Newton), bien que les deux penseurs semblent avoir développé leurs idées en même temps. Lorsque la Royal Society de Londres, dont le président à l’époque était Newton, a décidé qui a développé le calcul en premier, elle a attribué le mérite de la découverte du calcul à Newton, tandis que le mérite de la publication sur le calcul est allé à Leibniz. Leibniz a également été accusé d’avoir plagié le calcul de Newton, ce qui a laissé une marque négative permanente sur sa carrière. Le calcul de Leibniz différait de celui de Newton principalement par la notation. Fait intéressant, de nombreux étudiants en calcul aujourd’hui en sont venus à préférer la notation de Leibniz. Par exemple, de nombreux élèves utilisent aujourd’hui « dy/dx » pour indiquer une dérivée de y par rapport à x, et un symbole semblable à un « S » pour indiquer une intégrale. Newton, d’autre part, plaçait un point sur une variable, comme ẏ, pour indiquer une dérivée de y par rapport à s, et n’avait pas de notation cohérente pour l’intégration.
Leibniz a également redécouvert une méthode d’organisation des équations linéaires dans des tableaux ou des matrices, ce qui rend la manipulation de ces équations beaucoup plus facile. Une méthode similaire avait été découverte pour la première fois par des mathématiciens chinois des années auparavant, mais était tombée dans l’abandon.
Contributions à la philosophie
Monades et philosophie de l’esprit
Au 17ème siècle, René Descartes a mis en avant la notion de dualisme, dans laquelle l’esprit non physique était séparé du corps physique. Cela a soulevé la question de savoir comment exactement l’esprit et le corps sont liés l’un à l’autre. En réponse, certains philosophes ont dit que l’esprit ne pouvait être expliqué qu’en termes de matière physique. Leibniz, quant à lui, croyait que le monde était fait de «monades», qui ne sont pas faites de matière. Chaque monade, à son tour, a sa propre identité individuelle, ainsi que ses propres propriétés qui déterminent la façon dont elles sont perçues. Les monades, en outre, sont arrangées par Dieu – qui est aussi une monade – pour être ensemble en parfaite harmonie. Cela a établi les vues de Leibniz sur l’optimisme.
Optimisme
La contribution la plus célèbre de Leibniz à la philosophie est peut-être «l’optimisme», l’idée que le monde dans lequel nous vivons – qui englobe tout ce qui existe et a existé – est le «meilleur de tous les mondes possibles». L’idée est basée sur l’hypothèse que Dieu est un être bon et rationnel, et a considéré de nombreux autres mondes en plus de celui-ci avant de choisir celui-ci pour exister. Leibniz a expliqué le mal en déclarant qu’il peut entraîner un plus grand bien, même si un individu subit des conséquences négatives. Il croyait en outre que tout existait pour une raison. Et les humains, avec leur point de vue limité, ne peuvent pas voir le plus grand bien de leur point de vue restreint. Les idées de Leibniz ont été popularisées par l’écrivain français Voltaire, qui n’était pas d’accord avec Leibniz sur le fait que les humains vivent dans le « meilleur des mondes possibles ». Le livre satirique de Voltaire, Candide, ridiculise cette notion en introduisant le personnage de Pangloss, qui croit que tout va pour le mieux malgré toutes les choses négatives qui se passent dans le monde.
Un des objectifs de toute une vie de Leibniz était de rassembler toutes les connaissances humaines. Certes, il considérait son travail sur le droit civil romain comme faisant partie de ce schéma et comme une autre partie de ce schéma, Leibniz a essayé de rassembler les travaux des sociétés savantes pour coordonner les recherches. Leibniz a commencé à étudier le mouvement, et bien qu’il ait eu à l’esprit le problème d’expliquer les résultats de Wren et Huygens sur les collisions élastiques, il a commencé par des idées abstraites de mouvement. En 1671, il publie Hypothesis Physica Nova. Dans cet ouvrage, il affirmait, comme l’avait fait Kepler, que le mouvement dépend de l’action d’un esprit. Il a communiqué avec Oldenburg, le secrétaire de la Royal Society of London, et a dédié certains de ses travaux scientifiques à la Royal Society et à l’Académie de Paris. Leibniz était également en contact avec Carcavi, le bibliothécaire royal de Paris.
Leibniz a mis beaucoup d’énergie à promouvoir les sociétés savantes. Il a participé à des démarches pour créer des académies à Berlin, Dresde, Vienne et Saint-Pétersbourg. Il a commencé une campagne pour une académie à Berlin en 1695, il a visité Berlin en 1698 dans le cadre de ses efforts et lors d’une autre visite en 1700, il a finalement persuadé Friedrich de fonder la Société des sciences de Brandebourg le 11 juillet. Leibniz a été nommé son premier président, ceci étant un rendez-vous pour la vie. Cependant, l’Académie n’a pas été particulièrement réussie et un seul volume des actes a été publié. Cela a conduit à la création de l’Académie de Berlin quelques années plus tard.
Gottfried Wilhelm Leibniz (1646-1716)
Tenant une place intégrale dans l’histoire des mathématiques et de la philosophie, Leibniz était responsable de la création du calcul différentiel et intégral, avec Isaac Newton. La notation de Leibniz a été largement utilisée depuis. Leibniz est devenu plus tard l’un des inventeurs les plus prolifiques de calculatrices mathématiques. Au-delà de cela, il a apporté des contributions majeures à la philosophie avec son optimisme philosophique, bien qu’il ait écrit sur un vaste éventail de sujets au cours de sa vie.
Philosophe, mathématicien et conseiller politique allemand, important à la fois en tant que métaphysicien et en tant que logicien, et également distingué pour son invention indépendante du calcul différentiel et intégral. En rencontrant des universitaires tels que Christiaan Huygens à Paris et des membres de la Royal Society, dont Robert Boyle, lors de deux voyages à Londres en 1673 et 1676, Leibniz a été initié aux problèmes en suspens auxquels sont confrontés les mathématiciens et les physiciens d’Europe. Le calcul différentiel et intégral de Leibniz a découvert indépendamment (publié en 1684), mais s’est impliqué dans une amère dispute de priorité avec Isaac Newton, dont les idées sur le calcul ont été développées plus tôt (1665), mais publiées plus tard (1687).
Événements historiques
1675-10-29 Gottfried Wilhelm Leibniz fait la première utilisation du s long, ∫, pour intégral, aidant à découvrir le calcul intégral et différentiel
11/11/1675 Le mathématicien allemand Gottfried Wilhelm Leibniz démontre pour la première fois le calcul intégral pour trouver l’aire sous le graphique de la fonction y = f(x)
https://www.thoughtco.com/gottfried-wilhelm-leibniz-4588248
https://www.onthisday.com/people/gottfried-wilhelm-leibniz
https://mathshistory.st-andrews.ac.uk/Biographies/Leibniz/