Fasciné par les maxima et les minima des fonctions, Lagrange est le principal fondateur du calcul des variations.
Joseph-Louis Lagrange (1736-1813), mathématicien et astronome (théorie des nombres, mécanique céleste)
À 16 ans, il a commencé à étudier les mathématiques par lui-même et à 19 ans, il a été nommé professeur à l’École royale d’artillerie de Turin. L’année suivante, Lagrange envoya à Euler une meilleure solution qu’il avait découverte pour dériver l’équation centrale dans le calcul des variations. Ces solutions et leurs applications à la mécanique céleste par Lagrange étaient si monumentales qu’à 25 ans, il était considéré par nombre de ses contemporains comme le plus grand mathématicien vivant.
Très rapidement, il obtient des résultats probants. A l’été 1755, deux ans seulement après le début de ses travaux, il écrit une longue lettre à Euler (alors le plus grand mathématicien vivant) sur la détermination de la courbe tautochrone (i.e. la courbe telle que deux mobiles identiques lâchés au même moment en des points différents de la courbe arrivent au point le plus bas au même moment). Cette courbe (une cycloïde) a été déterminée pour la première fois par Huyghens, mais la méthode que propose Lagrange pour l’obtenir est beaucoup plus générale, et donnera naissance au « Calcul des variations ». Cet échange est le prémice d’une riche correspondance entre Lagrange et Euler, marquée par un respect mutuel important.
À la fin de cette même année 1755, Lagrange devient professeur à l’école d’artillerie de Turin., ville où il fonde en 1757 une académie des sciences. Son talent est très vite reconnu, et il écrit durant ses premières années de brillants mémoires où il applique les méthodes du calcul des variations à la mécanique (propagation du son, problème des n-corps, cordes vibrantes).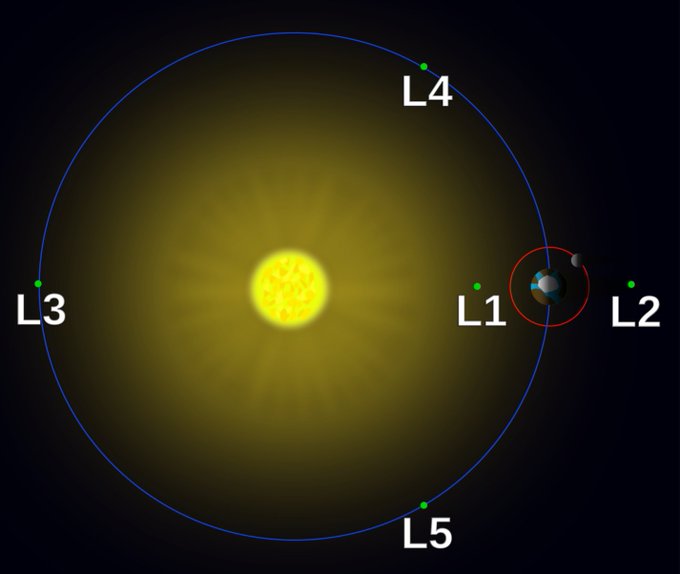 
En 1766, grâce à l’appui de D’Alembert, Lagrange succède à Euler au poste prestigieux de directeur des mathématiques à l’Académie des Sciences de Berlin. Il passera 20 ans là-bas, d’une extraordinaire fertilité. Hormis quelques arrêts dus à une santé fragile, il publie avec une régularité impressionnante des mémoires qui touchent tous les domaines des mathématiques et de la mécanique : astronomie, probabilités, théorie des équations algébriques (son travail sur les racines ouvre la voie à Abel et Galois), équations différentielles, théorie des fonctions.
Joseph-Louis Lagrange (1736-1813) Γεννηθηκε 25 Ιανουαριου. Ο υπολογισμος των σημειων Lagrange βοηθησε τη NASA. Αν σε ένα από αυτά τα σημεία τοποθετηθεί ένας δορυφόρος, θα δέχεται συνολική βαρυτική δύναμη μηδέν, αν συνυπολογιστεί και η φυγόκεντρος δύναμη. pic.twitter.com/uyAvj4rxBe
— evriWorks (@evriWorks) January 25, 2022
Lagrange excelle particulièrement en arithmétique, en résolvant plusieurs conjectures difficiles dues à Fermat, et en prouvant que tout entier naturel est somme de 4 carrés. Dans une perspective plus historique, Lagrange est à la transition entre l’époque d’Euler, où l’on publie à tout va sans trop se soucier de la rigueur, et le XIXe siècle, où sous l’impulsion de Gauss, Cauchy et Weierstrass, la rigueur devient un élément central des mathématiques.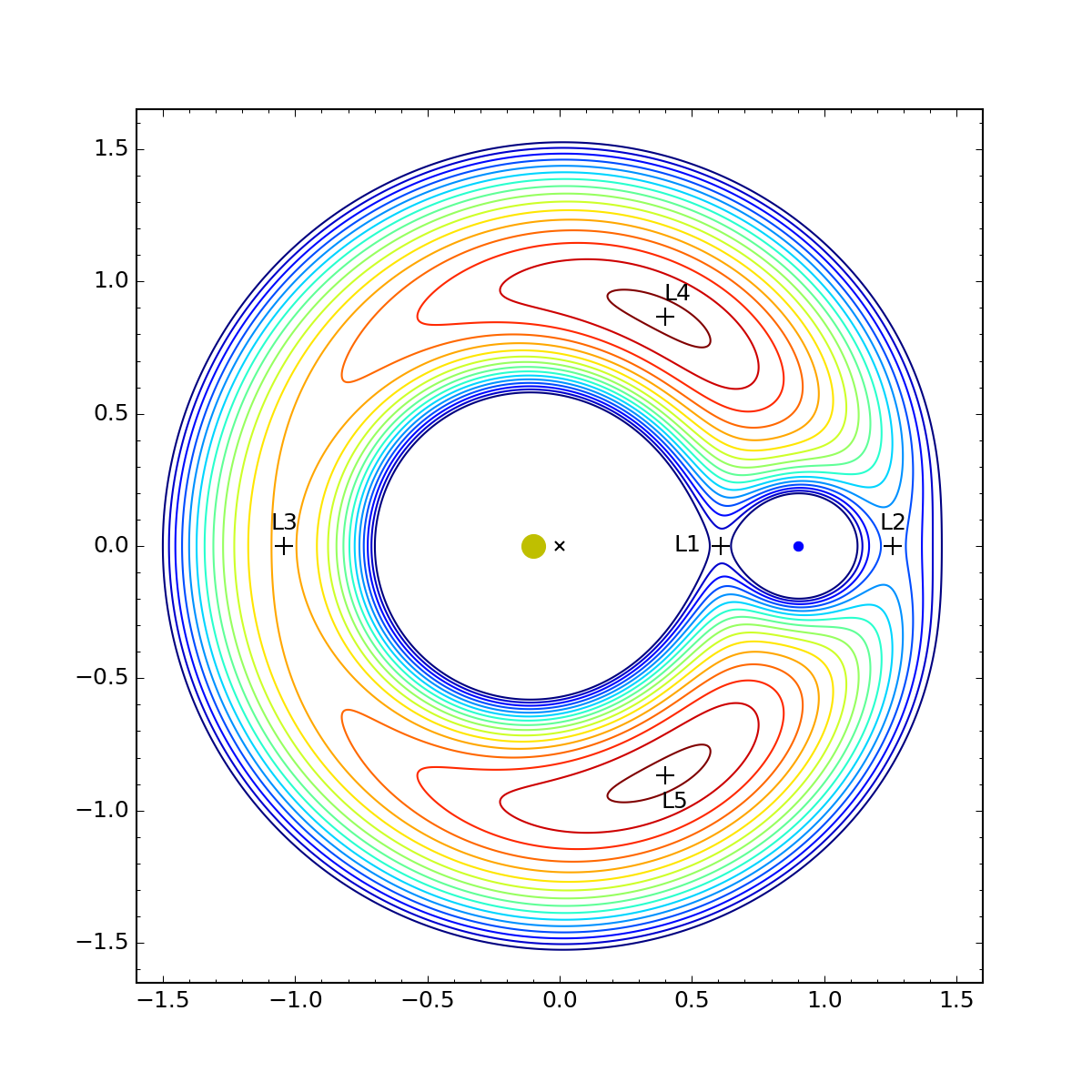
Joseph-Louis Lagrange est un géant de l’histoire des mathématiques. Il a apporté des contributions majeures au développement de la physique, de la mécanique céleste, du calcul, de l’algèbre, de la théorie des nombres et de la théorie des groupes. Il était en grande partie autodidacte et n’a pas obtenu de diplôme universitaire.
Fasciné par les maxima et les minima des fonctions, Lagrange est le principal fondateur du calcul des variations.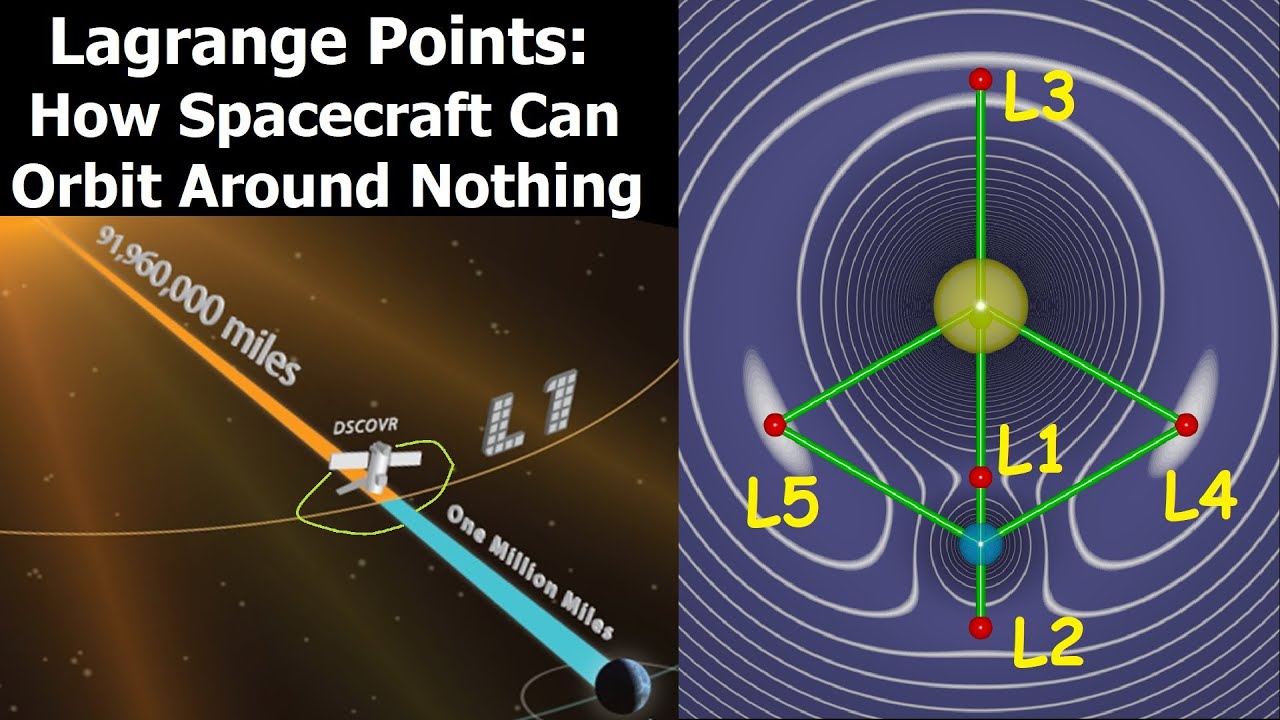
Dans une reformulation de grande envergure des lois d’Isaac Newton, Lagrange a créé une nouvelle vision brillante de la mécanique. Il l’a fait en utilisant le calcul des variations pour révéler les vastes implications d’un seul principe physique, le travail virtuel. L’un des résultats en fut la fonction lagrangienne, indispensable en physique avancée, calculée en soustrayant l’énergie potentielle de l’énergie cinétique.
La vision de Lagrange était entièrement basée sur l’algèbre et le calcul. Il croyait que c’était plus rigoureux mathématiquement que les idées intuitives générées par la géométrie. Il jugeait que ses méthodes situaient la mécanique dans le domaine des mathématiques pures.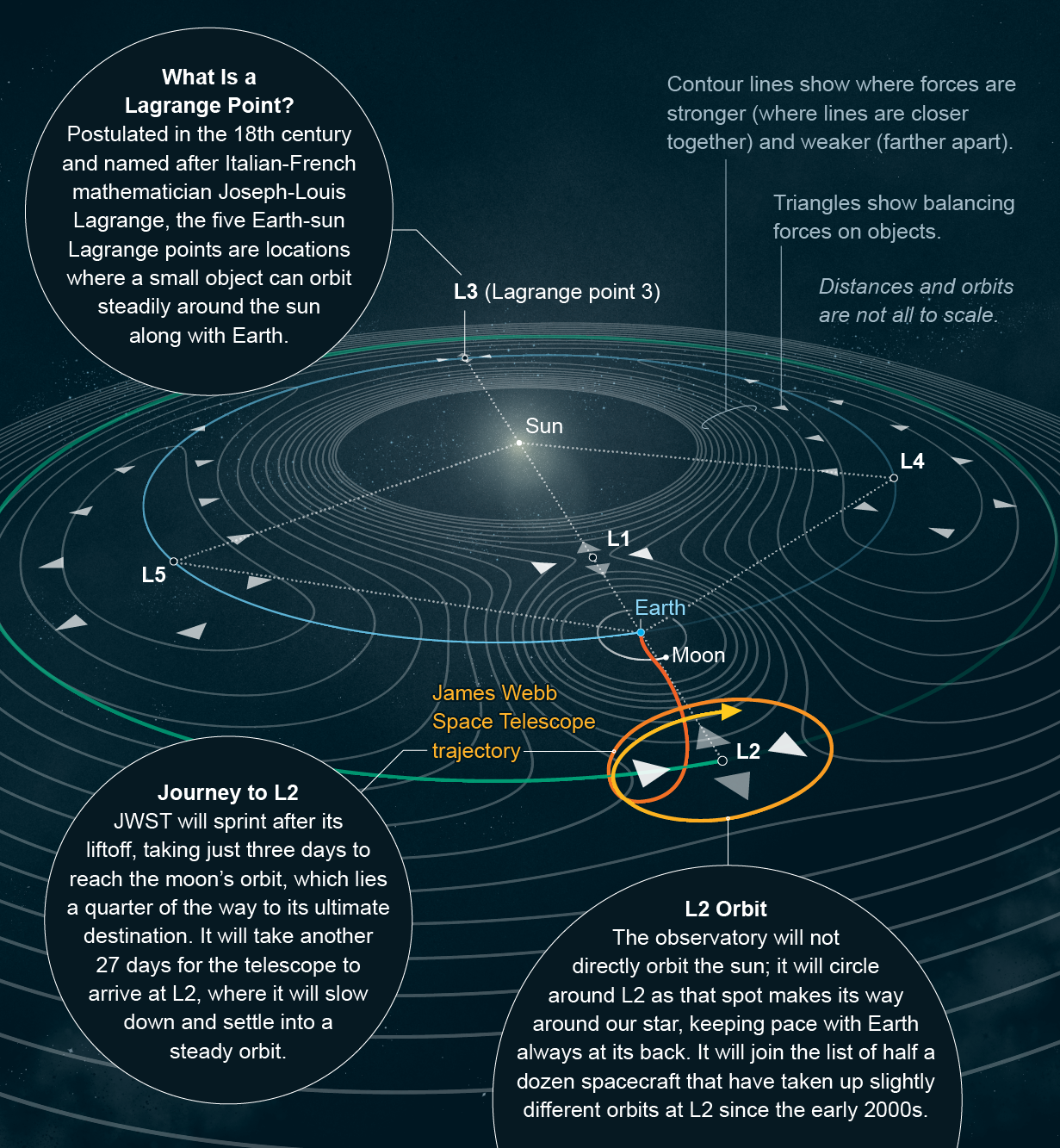
En mécanique céleste, Lagrange a découvert les points de Lagrange, appréciés également des auteurs de science-fiction et des planificateurs d’observatoires et de stations spatiales.
Lagrange nous a donné la notation familière f′(x) pour représenter la dérivée d’une fonction, f′′(x) une dérivée seconde, etc., et c’est d’ailleurs lui qui nous a donné le mot dérivée.
Réalisations et points clés
Construit sur les travaux antérieurs de Leonhard Euler pour créer le calcul des variations – il l’a appelé sa «méthode des variations».
Introduction de la notation ∂ et création des premières équations aux dérivées partielles.
A donné l’énoncé le plus généralisé du principe de moindre action de son époque.
Création d’un tout nouveau domaine de la mécanique, la mécanique lagrangienne, pour les solides et les fluides, basée sur le concept de travail virtuel et utilisant la fonction lagrangienne.
Introduction du concept de coordonnées généralisées. La mécanique lagrangienne peut être utilisée dans n’importe quel système de coordonnées – les problèmes sont simplifiés en choisissant celui qui convient.
Création du concept de potentiel : le champ gravitationnel, par exemple, est un champ potentiel.
Découverte des orbites lagrangiennes.
Résolution de problèmes séculaires en théorie des nombres posés par Fermat qui avaient vaincu d’autres mathématiciens.
A été l’un des fondateurs de la théorie des groupes.
A joué un rôle clé dans la création du système métrique des poids et mesures.
Les entrées du Dicomaths correspondant à Lagrange
Equations différentielles particulières
Extrema liés – Multiplicateurs de Lagrange
Formules de Taylor
Identité de Lagrange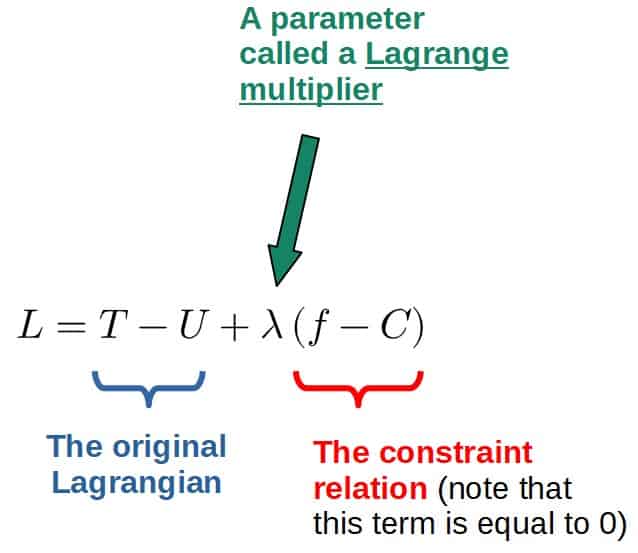
Méthode de Lagrange (ou fausse position)
Polynômes interpolateurs de Lagrange
Produit vectoriel
Théorème de Lagrange
Joseph Louis Lagrange (1736-1813)
https://www.bibmath.net/bios/index.php?action=affiche&quoi=lagrange